Te nem érted a kérdést. Ha a körvezetőben szerepel a sugár, akkor a körvezetőkből készített egyenes tekercsben miért nem?

Pislogok csak.

Ez mind világos, de a kérdés attól még változatlan. Logikusan azt várná az ember, hogy a nagyobb átmérőjű tekercs belsejében jobban eloszlik ugyanaz a fluxus, tehát abban kisebb lesz a fluxussűrűség. De valamiért mégsem lesz kisebb. A kérdés, hogy ennek mi az oka.

Igen, valóban az a közelítés, hogy a tekercs belsejében homogén tér van. De ez még mindig nem jelenti azt (és nem is magyarázza), hogy ennek a térnek a sűrűsége miért független a tekercs átmérőjétől, amikor minden más típusú huzalozásnál függ tőle.

A fluxussűrűség az indukcióval egyenlő. Ha van egy trafód, annak a vaskeresztmetszete mondjuk 10 ncm és ehhez tartozik mondjuk 1 Tesla indukció, vagyis B=1T. Ha megnöveled a vaskeresztmetszetet, akkor az indukció fordítottan arányosan csökken.

Itt a képlet hozzá: Fluxus ( fi ) = B x A. Ha a keresztmetszetet növeled, akkor csökken a B, hiszen a fluxus állandó. ( feltéve, ha közben marad a feszültség és a frekvencia.

Miből látod azt, hogy a fluxussűrűség nem lesz kisebb? De, kisebb lesz. Mi az a képlet amit emlegettek?

Ezt kérdezem én is:
"...De valamiért mégsem lesz kisebb." - hol van egy konkrét mérés, teszt?

A térerősség/grejesztés nem függ az átmérőtől.

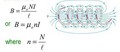
B=(µ0 * N * I)/l

A fluxus függ a területtől:

fi = B * A

A keveredés onnan eredhet, hogy a köznyelvben a "térerő" a mobilozáshoz kötött fogalom (bázisállomástól távolodva csökken).

Pontosan. Én is ezt a logikát keresném a képletben, csakhogy hiányzik belőle. A szolenoid indukciója ugyanis:

Bárhol. A mérés nyilván azt hozná, amit a képlet is állít, csak nem értem, hogy miért.

Helyesek a képleteid. Viszont attól tartok, hogy a "keveredés" sokkal mélyebbről ered. Itt nem egy egyszerű értelmezési problémával állunk szemben. Itt valami fundamentális dolognak kell lennie a háttérben, hiszen a józan paraszti ésszel teljesen ellentétes dolgot állít a képlet. Nem tudom ennél jobban megfogalmazni: ha egy vezetékhurok indukciója a képlet szerint fordítottan arányos a hurok sugarával (teljesen logikusan, hiszen ha változik a sugár, akkor ugyanaz a fluxus más és más fluxussűrűséget kell, hogy adjon), akkor a hurkokból összerakott szolenoid indukciója miért lesz független a mag sugarától? Mi az a dolog, ami a hurkok tekerccsé történő összerakása során megszünteti az indukció függését a sugártól?

Ez nem az indukció értékét adja meg, hanem a térerőét. ( Am mértékegységben. )

Erről nagy fizikusok nyilatkoztak, nem biztos, hogy jól el tudom magyarázni.

A tekercs gerjeszt egy bizonyos mértékű mágneses teret. Ez a mágneses tér eloszlik a tekercs belsejében de az már teljesen mindegy, hogy a tekercsnek mekkora az átmérője, a gerjesztés állandó és homogén, miközben a "sűrűsége", "ereje" nem. Utóbbi a fluxus, ami akár sűrű is lehet emberi léptékkel nézve. Legalábbis ideális tekercs esetén.

Nagyobb tekercs besejében kisebb mágneses erőt mérnél, miközben a gerjesztés mindkét tekercs esetében egyezik.

Tévedés. A mágneses térerősség (nem térerő) mértékegysége Amper/méter. A mágneses fluxussűrűség (B) mértékegysége Tesla. Ez utóbbiról beszélünk most. És de, ez a képlet a B értékét adja meg, oda is van írva.

Megtennéd, hogy leírod, hogy az egyes tagok ebben a törtben milyen mértékegységekkel rendelkeznek? Ha azokkal elvégzed a kijelölt műveletet, akkor valóban A/m-t kapsz. De ugye ez nem az indukció?

Már hogyan lenne mindegy? Ott a hurokvezető képletében a sugárfüggés. A mező valóban homogén a szolenoid belsejében, de ezt még nem jelenti azt automatikusan, hogy független is a sugártól. Sőt! A homogén mágneses mező fluxusa teljesen egyértelműen függ a felülettől (tehát a sugártól is), Te magad tetted be a képletet róla. Szóval nem tudom, hogy a nagy fizikusok mit nyilatkoztak, de akármi is volt az, egyhurkú vezetőre miért nem érvényes?

Ez itt egy komoly elméleti probléma, és látszik, hogy ez elsősorban egy gyakorlati szakikat tömörítő fórum. Valahogy nem esik le senkinek, hogy itt valami nagy szar van a palacsintában.

De, az. Mágneses indukció (vagy más néven mágneses fluxussűrűség), jele B, mértékegysége Tesla, vagy másképp V*s/négyzetméter.
A: felület (négyzetméter)
R: sugár (méter)
N: menetszám (nincs dimenziója)
l: hossz (méter)
I: áram (Amper)

Én az általad becsatolt 01.jpg képen található képletről beszélek. Az nem az indukciót fogja megadni.

Nincs itt probléma. A

B=(µ0 * N * I)/l

képlet a gerjesztés mértékét adja meg. Képzeld úgy, mintha a végeredény literben lenne mérhető. Van x mennyiségű vized, ez csak úgy lebeg a térben. Ezt a mennyiségű vizet a tekercsen átfolyó áram hozta létre. Ez független attól, hogy milyen átmérőjű a tekercs. Ha az x mennyiségű vizet kiöntöd egy tálba, alacsony vízszintet kapsz, ha vázába borítod (kisebb átmérőjű tekercs), magasabbat.

Egy egyenes vezetőnél a mágneses tér metszete kör alakú. Egy huroknál két kört fogsz látni, de egy tekercsnél már van egyenes szakasz is.

Dehogynem. Húszmillió példányban fenn van a neten a képlet, itt egy másik:

Ha nem vagy hajlandó még átgondolni sem amit javasoltam, sosem fogod megérteni.
Nyilván te jobban hiszel a neten levő húszmilliónak, mint a saját tudásodnak. Ehhez nem kell túl sok minden... Leírtam, mit csinálj.

Csak tényleg zárójelben: a középkorban az emberek óriási többsége azt vallotta, hogy a Föld lapos. Csak egy maréknyi ember volt, aki tudta, hogy gömbölyű. Érdekes módon nem az óriási többségnek lett igaza...

Már hogyne lenne probléma? Hiányzik a sugár a képletből, tehát egy ház-méretű tekercsnek is ugyanakkora lenne az indukciója azonos áram és menetszám esetén, mint egy kisujjnyinak? Ne már.
Rossz a hasonlatod, hiszen itt pont az egységnyi felületre eső vízről beszélünk, nem pedig magáról a vízről. A víz a fluxus lenne, de mi most a felületegységre eső fluxusról, vagyis a fluxussűrűségről beszélünk.
Igen, a mező alakjával kapcsolatban igazad van. De ez még mindig nem ad választ a kérdésre.
Amúgy köszi mindenkinek az együtt gondolkodást, érdekes dologba futottunk bele.

Ácsi-ácsi, ugye nem azt akarod mondani, hogy hibás a képlet, ami MINDEN fizikakönyvben szerepel? És de, pont azért problémázok itt, mert a saját tudásomnak szeretnék hinni, az viszont ellentétben áll azzal a képletben, amely alapján minden működő cuccot megterveztek az utóbbi elég sok évtizedben.

Figyelem! Figyelem! Szolgálati közlemény! Az ügyeletes fizikaprofesszort sürgősen várják a Tekercsek c. topikba!

A vitatkozás helyett inkább számold ki, hogy ez a képlet milyen mértékegységet ad. Elárulom: A/m. Ugye az indukció mértékegysége a Tesla, ami azt jelenti, hogy egy VS/nm. Ezt te magad is leírtad... Legyél kicsit konstruktívabb.

Tényleg nem értem amúgy, mi nem érthető. Nézzétek meg a legutóbbi képet, ott az a szép kis tekercs. Növeljük meg a sugarát (húzzuk szét) úgyhogy a többi paraméter (áram, hossz, menetszám) állandó marad. Ilyenkor az mondaná a logika, hogy a mágneses tér is megritkul, "széthúzódik". A képlet szerint viszont nem, tehát ugyanolyan sűrű marad. Vagyis ahányszorosára nő a keresztmetszet, valami miatt annyiszorosára nő a tekercsben a mágneses erővonalak száma. Tehát így marad ugyanakkora a B. De hogy lehet ez? Mitől jönne létre több erővonal? Ha a sima hurokban nem jön létre több erővonal ilyenkor, akkor a szolenoidban miért igen? Kérlek, mondjátok, hogy értitek a kérdést.

Hát kb. Ide valami elméleti szakember kell.

Tévedés. Ez a képlet pontosan azt adja ki, amit ki kell adnia: Vs/nm-t. Nézd csak:

B=[Vs/Am]*[-]*[A]/m ===> B[Vs/nm]

(Ne feledd, a permeabilitásnak is van mértékegysége!)

VS/nm = voltsiemens per nanométer.

Igen. A probléma csak az, hogy a 01.jpg képletben a nevezőben nagy "EL" van ami az induktivitás jele.
Amit később belinkeltél, ott a nevezőben kis "el" van. Van egy kis különbség.

Igen, elcsesztem a kis s-t... mea culpa...