Fórum témák
» Több friss téma |
köszi! Digitális technika házit gépen akartam megcsinálni, hogy amikor beadom, akkor szépen, nyomtatásban legyen, de akkor inkább majd szépen lerajzolom, ennyit nem ér meg!
ha segit a dolog:
ms office (xp, de sztem többi alatt is) a beszúrás (insert) -) objektum (object) ben van. microsoft equation a progi neve. vagy más néven math type. gl2hw.
Sziasztok.
Kaptam ezt a feladatot és nem tudo megcsinálni. Y(X3,X2,X1X0)=SUM(4,5H,7,8,12,13). Ezt a hálozatot kéne megalkotnom. Én minterm táblával csináltam sztem csak ezzel kell. NAND-AND kapuk használatával. Micro-cap 9.0-ás softwaret használok és nekem nem jött ki. Ott is világított ahol nem kellett volna. A lefedést sztem nem szúrtam el lehet a függvény felírásával van valami probléma, nem tudom :S Előre is köszi a segítséget Üdv Alan
NAND-AND kapukkal?
NAND kapukkal fel lehet írni minden fv-t. Nem értem akkor miért kell bele AND kapu? Kötelező, hogy legyen benne AND?
Én így képzeltem el, de ez nem jó, mert világít ott is ahol nemkéne
Nekem ez jött ki:
A: MSB D: LSB ((ABnDn)n*(BCn)n*(AnBDn)n)n Ami ugyanaz mint amit megrajzoltál. Tehát az egyszerűsítés jó. A microcaphoz nem értek.
Remélem, jól értelmeztem a feladatot. Én felrajzoltam Karnaugh-táblákkal, kiírtam az alapján egy egyszerűsített kombinációs függvényt, ez lett:
Y = X3*!X0*!X1 + X2*!X1 + X0*!X3*X2 A tiedből pedig ez írható fel: !Q = U1*!U4*U3 + !U2*U3 + !U1*!U2*U4 Ezt visszarajzolva Karnaugh-táblába azt látom, hogy szerintem X3..X0 -> U4..U1 helyettesítéssel jól oldottad meg Te is, a táblák ugyanúgy néznek ki, csak nálad a kimenet negált. A kimenetre is NAND kellene, akkor ponált lenne az is. Azután meg az invertereket is lehet NAND-dal helyettesíteni, így végül nem is kell más kapu.
Igen tudom, hogy NAND-NAND kapukkal működne.
CSak az a baj, hogy ez a házi feladatom, és mindenféleképpen NAND-AND kapukkalkell megoldanom.
Akkor a kimeneti and után tegyél még egy invertert, NAND kapuból kialakítva
 Vagy a bemenetek invertáltjait is alakítsd ki NAND-okból. A szorzatok előállítása után mindenképpen egy OR kapcsolatot kell összerakni, azt AND és NAND elemekből csak úgy lehet, ha egy AND kapu bemeneteit és kimenetét is invertálod, mondjuk NAND kapukból kialakított inverterekkel. De az elég hülyén fog kinézni.
OKés köszi. Megpróbálom és akkor majd beírom, ha sikerült vagy ne adja isten nem sikerülne

Így se megy :S
6,9,12,15-nél is világít pedig ott nem kéne 
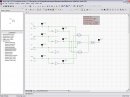
Megcsináltam Tinában.
Jó és működik. Mintermes karnaugh tábla, egyszerűsítés, amiből kijön amit szilva írt. Az előző hsz-ben írt képletem nem jó, valamit elszámoltam.
Áhhh köszi. Így jó lett!!!! Nagyon nagy köszönet érte.
Tényleg az életemet mentetted meg  . Köszi! . Köszi!
Be tudnád tenni valami képként is, hogy hogy néz ki a végleges?
persze. Nekem így néz ki. LED-es tesztel kijött minden érték. A végére kell az inverter.
Kellene egy kis elméleti segítség ebben a témába.
 Segítenétek levezetni a 74141 es dekóder igazságtábláját (tábláit). Elsősorban a tálázat levezetése érdekelne!
Van 10 kimeneted (0-9). Ezekre mindegyikre fel kell írni egy egy karnaugh táblát az igazságtáblázat alapján. Ezeket egyszerűsíted, és kész a megoldás.
Ez eddig OK.
 [off]DE Elég tömörre sikerült a válasz...  Lehet h túl könnyű IC-t választottam!? Lehet h túl könnyű IC-t választottam!?
Mivel van konkrétan problémád?
A függvények egyszerűsítése, vagy az igazságtábla felírása okoz gondot?
Valaki le tudná vezetni nekem, ezt hogy lehet leprogramozni C nyelven?
A logikára lennék kíváncsi és az egymás utáni folyamatokra. 8 bemeneti változóig szeretném működésre bírni a programot. Előre is köszönöm! 
Sziasztok!
Segítséget szeretnék kérni mert nekem nagyon nem megy ez a Karnaugh tábla. Addig eljutok, hogy felrajzolom, címezem, beírom az értékeket, de a termek összevonása sem látható számomra. Adott egy feladat nem teljesen specifikált hálózatra: 1: (3,4,615) nem számít: (5,7,11) Elvileg a megoldás: |A*B + CD Nos én ezt csak nagyon hosszú írogatás után kapom meg és ránézve a táblára nem értem, hogy miért ez a megoldás. Levezetné nekem valaki? Ja igen annyi még, hogy NAND kapuval kell megretvezni a hálózatot. Hogyan látom a táblán, hogy NAND kapuk fognak kelleni?
Szia!
Itt van egy ilyen tábla. A bal felső darkokban lévő számokhoz pedig "1"-es kell rakni, ha szerepel a szám a függvényben. Tehát esetünkben a 3,4,6,15-ös számokhoz kell 1-et írni. Utána hurkokat kell csinálni, be kell karikázni azokat a csoportokat, amelyek függőlegesen vagy vízszintesen összetartoznak. A lényeg, hogy minél több ilyen hurok legyen. Egy hurokban csak 2^n db szám lehet. Esetünkben az 5,7,11-es számokhoz is lehet 1-est írni, ha segítik a hurkok létrehozását. NAND kapuval pedig úgy lehet megoldani, hogy létrehozol NAND kapukkal AND és OR kapukat. De mindjárt lerajzolom, hogy jobban megértsd.  Szerk.: a megoldásnál az "A" az negálva van, az "A" és "B" közt pedig ÉS kapcsolat van?
Ezt a fajta peremezést nem ismerem.
Az a baj, hogy a tanárunk teljesen más peremezést használ mint amiket a neten látok. Addig eljutok, hogy felrajzolom és kitöltöm a táblát bekarikázom a termeket. A kivolvasás nem megy egyáltalán. :no:
Hello!
Először a tábla helyes felállítását kell megcsinálni a súlyozás szerint. A mellékelt file-ban jól látható. A súlyozásra nincs benne példa. Másodszor, tisztában kell lenni azzal a szabállyal ami alapján létre lehet hozni az egyes hurkokat. A Karnaugh táblában a hurkokban lévő "termek" ÉS kapcsolatban vannak egymással. A hurkok pedig vagy kapcsolatban lesznek. Ebből az látszik, hogy a kimenet az egy VAGY kapu eredménye lesz. Az AND kapus eredmény az egy Veitch tábla eredménye lesz ami a Karnaugh tábla ellentettje (excel tábla). Üdv.
Részben kapizsgálom amit írsz. Az a baj, hogy arról semmi nem hangzott el a konzultációkon, hogy milyen szabályok szerinte kell eljárni és a jegyzetünkben sincs benne. Egyből azzal indít, hogy ezt úgyis tudjuk.
A mellékelt peremezés szerint kell használnunk. Erre a formára szinte sehol sem találok példát. Persze elvileg az a lényeg, hogy a megfelelő címekre vegyem fel az (1) értéket. |
Bejelentkezés
Hirdetés |