OK Mégsem
Fórum témák

» Több friss téma
Cikkek » MMA7260QT gyorsulásmérő használata AVR-rel
MMA7260QT gyorsulásmérő használata AVR-rel
Szerző: Fizikus, idő: Szept 21, 2010, Olvasva: 25841, Oldal olvasási idő: kb. 2 perc
Lapozás: OK   7 / 9

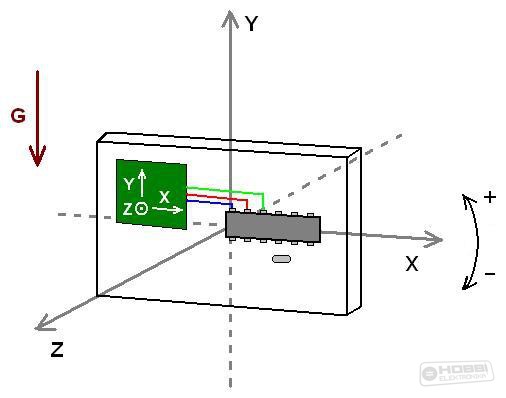
Ha egy tárgy dőlésszögét egy adott tengely irányában meg akarjuk határozni, akkor nincs mese, elő kell venni a középiskolás négyjegyű függvénytáblázatot, és fel kell eleveníteni a trigonometrikus függvényekről tanultakat (LINK). Ha csak lassan változó mozgásokat vizsgálunk (pl. egy tárgy dőlésszögének vizsgálata ilyen), akkor a gyorsulásmérő a G gravitációs gyorsulás X, Y és Z tengely irányú komponensét méri. Ezekből az értékekből kell a dőlésszöget meghatározni.

Nézzük meg, ez hogyan lehetséges 1 tengely mentén!

A gyorsulásmérőt az alábbi ábrán látható függőleges elrendezésben fogom használni:

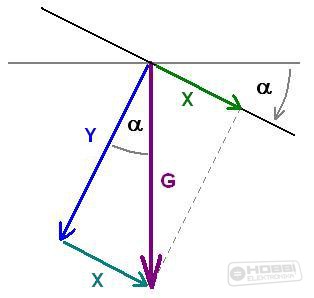
Ekkor egy negatív irányú, alfa szögű dőlésszög esetén a G gravitációs gyorsulás X és Y tengely irányú komponensét az alábbi ábra mutatja:

A szenzor az Y és a Z irányú gyorsulást méri. Ahhoz, hogy ezekből a mért értékekből a különböző irányok mentén tapasztalható dőlésszöget megkapjuk, egy-két trigonometriai számítást kell elvégeznünk.

X=G*sin(alpha)

Y=G*cos(alpha)

X/Y = tan(alpha)

alpha = arctan(X/Y)

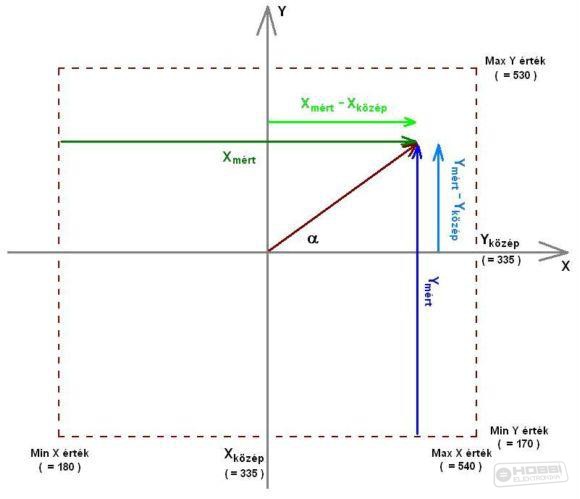
Tehát a mért értékekből az arkusz tangens függvénnyel tudjuk kiszámolni a dőlésszöget. De van egy kis probléma, a tangens függvény nincs értelmezve azoknál a szögeknél (pl. +/- 90o), amelyeknél a koszinusz függvény értéke nulla (nulla értéknél nincs értelmezve az osztás művelete). Egyes szögeknél pedig a szinusz és koszinusz függvények értéke negatív, ezért pl. +45o és a -135o (+225o) tangense is ugyanaz az érték. Ahhoz hogy a helyes dőlésszögértékeket kiszámoljuk, figyelembe kell venni az adott szöghöz tartozó szinusz és koszinusz függvények előjelét is. Ez csak tovább bonyolítja a dolgokat, de szerencsére a Processing tartalmaz egy ún. atan2(y,x) függvényt. Ez a függvény kiszámolja a paraméterként megadott  (x,y) koordinátákból a koordináta rendszer középpontjába mutató irányvektor dőlésszögét, és azt is figyelembe veszi, hogy x és y értéke negatív bizonyos dőlésszögek esetén.

Ennek a függvénynek a használatával nagymértékben leegyszerűsödik a dolgunk, mert a fenti ábrán feltüntetett módon, a mért értékekből kiszámolható a dőlésszög.

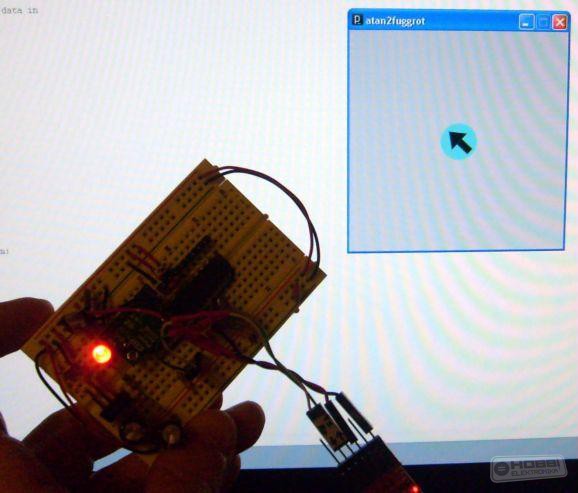
alpha = atan2({Y_{mert} - Y_{kozep} }/ {X_{mert} - X_{kozep}})

Ezt felhasználva, készítettem az alábbi Processing példaprogramot, ami a képernyőn megjelenít egy, a kiszámolt dőlésszög értékkel elforgatott nyilat.
 

(a videóhoz kattints a képre)

Processing kód:

  1. import processing.serial.*;      // soros portokat kezelo konyvtar importalasa
  2. int graphPosition = 0;           // nyil kezdeti poziciojanak megadasa
  3. int[] vals = new int[3];         // gyorsulasmero altal mert ertekek
  4. int[] maximum = new int[3];      // maximum ertekek
  5. int[] minimum = new int[3];      // minimum ertekek
  6. int[] mid = new int[3];        // kozepertekek
  7. float position;                
  8. Serial myPort;                  
  9. boolean madeContact = false;    
  10.  
  11. void setup()
  12. {
  13.   background(255);
  14.   size(300, 300);        
  15.   // a kalibracioval mert maximum, minimum es kozepertekek megadasa
  16.   maximum[0] = 540;
  17.   minimum[0] = 180;
  18.   mid[0] = 335;
  19.  
  20.   maximum[1] = 530;
  21.   minimum[1] = 170;
  22.   mid[1] = 335;
  23.  
  24.   position = width/2;
  25.  
  26.   PFont myFont = createFont(PFont.list()[2], 14);
  27.   textFont(myFont);
  28.  
  29.   myPort = new Serial(this, Serial.list()[2], 9600);
  30.   myPort.bufferUntil('\n');
  31.  
  32.   noStroke();
  33.   smooth();
  34.    
  35. }
  36.  
  37. void draw()
  38. {
  39.   background(204);
  40.   if (madeContact == false)
  41.   {
  42.     myPort.write('m');
  43.   }
  44.   float a = atan2(mid[1] - vals[1], mid[0] - vals[0]);
  45.   // nyil kirajzolasa a mert dolesszoggel
  46.   drawArrow(a);
  47. }
  48.  
  49.  
  50. void drawArrow(float a)
  51. {
  52.   translate(width/2, height/2);
  53.   // vilagoskek kor kirajzolasa
  54.   fill(80,200,230);
  55.   ellipse(0,0,50,50);
  56.   // nyil szinenek (fekete) megadasa:
  57.   fill(0);
  58.   // dolesszoggel torteno forgatas
  59.   rotate(a - PI/2);
  60.  
  61.   // nyil megrajzolasa egy negyzettel es egy haromszoggel:
  62.   triangle(-15, 0, 0, -20, 15, 0);
  63.   rect(-5,0, 10,20);
  64. }
  65.  
  66. void serialEvent(Serial myPort) {
  67.   madeContact = true;
  68.   String myString = myPort.readStringUntil('\n');
  69.   if (myString != null)
  70. {
  71.     myString = trim(myString);
  72.     int sensors[] = int(split(myString, ','));
  73.  
  74.     if (sensors.length >= 3)
  75. {
  76.       vals[0] = sensors[0];
  77.       vals[1] = sensors[1];  
  78.       vals[2] = sensors[2];
  79.       delay(100);
  80.       myPort.write('m');
  81. //      delay(100);
  82.     }
  83.   }
  84. }


A cikk még nem ért véget, lapozz!
Következő: »»   7 / 9
Értékeléshez bejelentkezés szükséges!
Bejelentkezés

Belépés
Hirdetés
XDT.hu
Az oldalon sütiket használunk a helyes működéshez. Bővebb információt az adatvédelmi szabályzatban olvashatsz. Megértettem