Váltakozóáramú körökben a műszered által kijelzett érték egy effektív érték ami azt jelenti, hogy effektíve annyi mint egy ekkora (a kijelzett értékű) egyenáramnak az értéke! Tehát nem a "teljes" feszültség értékét kapod, mivel az 1,414-szerese a mért/kijelzett értéknek. De mivel ez egy időben változó mennyiség ezért az egyenáramhoz viszonyított értékét adják meg.

A pufferelés az okoz ilyet.

Azaz egyenirányítasz és pufferelsz akkor nem effektív feszkót kapsz, hanem többet emiatt van a kavarc amiről próbálsz írni nem?
Azaz ha egy pufferelt egyenoldalon 100mA el terheled a kész tápot akkor befelé mégis több áram folyik a graetz előtt...

Csak te mindenhol csak egyenirányítást írsz...

Persze, pufferelt egyenirányításra gondoltam.
Azért 1.41-ezek itt..
Szóval ha a pufferelt egyenirányításnál 100mA-t mérek, mennyit mérek egyenirányítás előtt ?
Ez volt a kérdés.

Sturbi leirta 4 hozzászólással lejjebb:



Ennél érthetőbben nem lehet megfogalmazni.
De ha nem hiszel neki, fogj egy multimétert,és mérd meg midkét oldalon az áramot. Úgy tűnik nemigen tudod értelmezni a dolgokat.

A puffer bonyolítja a megértést, de nem befolyásol alapvető törvényszerűségeket. Tisztázni kell mi a villamos áram a vezetőben és mi az áramerősség. A villamos áram a vezetőben nem más mint szabad elektronok mozgása. Az elektron az anyag egyik alkotórésze, amelynek a töltése "valamennyi" coulomb. 1 coulomb kb. 6 trillió elektront jelent. A villamos áram erőssége (áram) a vezető keresztmetszetén egy másodperc alatt áramló töltésmennyiség (elektron). Akkor 1 A az áramerősség, ha egy mp. alatt 1 C (kb. 6 trillió elektron) áramlik az illető keresztmetszeten. A fentiekből következik, hogy az áramerősséget megkapjuk ha elosztjuk a töltés mennyiségét a töltésáramlás idejével (I=Q/t). A nevezőben ott az idő. Úgy gondolom az nem lehet kérdéses, hogy ha a pufferből elvesz a terhelés 1 coulombnyi töltést, akkor az egyenirányító (és a trafó) felől a pufferbe (ami ez esetben a trafó terhelése) szintén 1 coulomb töltés fog kerülni. Állandósult állapotban (a puffer már fel van töltve és eltekintünk a veszteségétől is), és ha a puffert terhelő ellenállás pontosan megegyezik a puffert töltő ellenállással, és az ohm törvény alapján kikényszerített áramerősséget a körök ellenállása korlátozza (trafó belső ellenállása, diódák ellenállása, illetve másik oldalon a vele egyező nagyságú terhelő ellenállás) az áramerősség a két áramkörben (trafó-dióda-puffer/puffer-terhelés) mindig egyezni fog. A kapocsfeszültség a pufferen a vátófesz effektív értékével fog egyezni (nem gyök kettő-ször nagyobb), mintha a puffer ott sem lenne (a tápegység nem ilyen). Ha a trafó belső ellenállása kisebb, mint a fogyasztó ellenállása, akkor a puffert töltő áram erőssége nagyobb lehet a folyás alatt (folyási szöggel arányosan, ami viszont a puffer értékével is arányos), mint a pufferből elfolyó áram erőssége (nem a villamos áram, hanem annak erőssége (mert ott az idő a nevezőben)). Ez az alapvető oka annak is, hogy terhelten soha nem érhető el a csúcsfeszültség a pufferen (nem a különböző ohmikus veszteségek). -Hogy a pufferfeszültség mennyire közelít a csúcsfeszültséghez elsősorban azon múlik, hogy a tápegység (és legfőképp a trafó) belső ellenállása, a puffer nagysága, és a puffer terhelő ellenállása hogyan viszonyul egymáshoz (kis belső ellenállású trafó, nagy puffer (nagy töltő áramerősség), kis terhelés értelemszerűen nagyobb pufferfeszültséget okoz (a puffer tertalékot tud képezni a töltőkör kis belső ellenállása miatt)).
Remélem nagyon nem keveredtem bele...

Kösz !
Már értem. Szóval a pufferelt sem végez nagyobb munkát ( ), mint a nem pufferelt, csak más értéket mér az ember.
:wave:
Igazából csak trafó méretezéséhez kell, de már mindegy, mert megtekertem. (kicsit vastagabbal a trafót mint a fojtót)

Üdv!

Enyhén szólva belezavarodtam kicsit a dolgokba.
Az áramerősséget lényegében mi határozzuk meg?
Addig oké hogy egy ellenálláson változó fesz hatására változni fog az áram de mi a helyzet egy trafóval vagy a hálózattal?
Lehet 30-40 ampert is akár egy zsebtelepből kinyerni ennek értelmében? Vagy csak kis feszültség esetén a fesznél alacsonyabb áram jöhet létre?

Kösz. Most tök tiszta lett a fejem. Ezt tudom de amit írtam azokat nem értem.

És akkor hogy van az hogy egy trafó ennyivel egy másik meg annyival terhelhető?

Helo!
Egy trafó terhelhetősége függ: a vasmag méretétől és típusától és a rá feltekert huzal menetszámától és a huzal vastagságától. (Nagyvonalakban megfogalmazva)

A trafónál az átvihető teljesítmény elsősorban a vasmag méretétől függ. Pl. ha van egy 100 w-os trafód, amely 12 V-ot ad ki akkor legfeljebb I=P/U = 100 w/12V = 8.33 A-el terhelhető. 200 watt-os trafóból 12 V-nál már 16.6 A
vehető ki.

Üdv!

Na kezd tisztulni a kép. Köszönöm mindenkinek.

meg szeretnem tudni hogy hogyan tudom legegyszerubben egy tengely forgasabol elektromos aramot eloallitani? fontos lenne allamvizsgadolgozathoz kell...a legegyszerubb modozat erdekelne, reszletezve hogy meg tudjam csinalni a garazsban is...szeretnem ha valaszukat a *** .elore is koszonom

* Emil törölve .

bölcsész karon diplomázol?

Akkor legalább írnia kellene tudni

Megjegyezve hogy nem mindegy a fordulatszám, a legegyszerűbb ha a tengely végére csatlakoztatsz egy egyenáramú motort, pl. kazettás magnóét.
Van aztán a dörzselektromosság az is barkácsolható...

Elméletben ha fogok egy fűkaszát kiszedem a motorját és a motor főtengelyét hozzá erősítem egy generátorhoz azt meg egy motorhoz akkor elméletben sikerülhetne e meghajtani egy biciklit ( az ötletet a dízelmozdonyokból vetem) motor 9800ford/perc a generátor 14,5 volt és 45 ampert tud maximális fordulatszámon ami nem tudom hogy hol, egy 12volt 40 amperes motort a többi pedig a világítást ez így mekkora esélyem van ara hogy olcsóbban jövök ki mintha simán megvenném a benzint

Semennyi. Ezt a hajtást egyébként soros hibridnek nevezik. A gond, hogy a sok energiaátalakítás jelentősen csökkenti a hatásfokot. Igen jó hatásfokú villamos gépekkel sem lehet igazán jó eredményt elérni. A fő előnye ennek a módszernek, hogy a belső égésű motort optimális munkapontban lehet járatni. Optimalizálni lehet például a teljesítményre nyomatékra vagy az emisszióra. Szóval nem igazán érdemes ezzel foglalkozni. Jobb eredményt biztosan nem lehet vele elérni.

Üdvözletem!
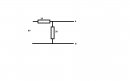
Lenne egy eléggé bárgyú feladatom, amit meg kellene oldani.(Melléklet) A kérdés az, hogy mekkora az A-B pontok közötti feszültség. A számítás menete érdekelne.
Köszönettel:Máté.

Ez egy feszültségosztó kapcsolás.
1k+2k=3k -> 9V / 3= 3V -> 2*3V=6V ---> A-B=6V
Ha nem érted akkor google, vagy keress egy könyvet. pl általános iskolás fizika.

Báddzsó már nagyon helyesen megállapította és kiszámította a feszültségosztó képlet alapján az eredményt.
A megoldóképlet onnan származik, hogy a két ellenállás sorosan van kapcsolva, tehát azonos nagyságú áram folyik át rajtuk. Ez az áram: I = 9V/(1k+2k). Mivel ismerjük az átfolyó áramot, valamint az ellenállás értékét, az A-B pontok közti feszültség Ohm törvénye alapján számítható: U = R*I, ebben az esetben U = 2k*I, vagyis U = [2k/(1k+2k)]*9 V = 6 V. Innen származik az úgynevezett feszültségosztó képlet.

Adatátvitelben találkoztam a Back To Back fogalommal, de nemtudom pontosan mit is jelent. Olyasmire gondolok, mikor az adatfolyam "nem ér véget", hanem rögtön kezdődik a következő csomag. Példaként az RS232 ben, mikor a stop bit után folyamatosan jön a start bit. Szóval mikor a csatorna full ki van használva. Ilyen kifejezést találtam ethernet hálózatokban is.
Árnyalja a képet, hogy olvastam egy műszerről, melynek egyik tulajdonságaként szerepeltetik a Back-to-Back Buffer -t.
Sajna google-n nem találtam korrekt magyarázatot a kifejezésre, de remélem Ti tudtok segíteni.

Sziasztok!

Lenne egy egyszerűnek tűnő kérdésem: Hogyan lehet kiszámítani egy soros RC kör ellenállásán létrejövő hőenergiát? Feltételezzük, hogy van mondjuk 2,2nF os kondenzátorral sorban 47ohm. A kondenzátor kezdeti feszültsége 0V, és hirtelen 200V-ot kapcsolunk az RC körre.
A kérdés az lenne igazából, hogy egy feltöltés alatt mennyivel nő meg az ellenállás hőenergiája. Ezt sajnos nem tudom kiszámítani, de úgy tippelem, hogy ha ki lehetne integrálni 5TAU időre az ellenállás áramának négyzetes középértékét (RMS), abból könnyedén ki lehetne számítani, ha ezt az effektív áramot négyzetre emelnénk, szoroznánk R-rel, és beszoroznánk 5TAU idővel.

Arra gondoltam, hogy az i=I0*e^ -(t/TAU) összefüggés négyzetét kéne integrálni. Ebből I0 a kezdeti áram (Ut/R), i az áram pillanatértéke, az " e " természetesen az Euler-féle szám, 2,718...

Lineáris közelítések kilőve. Táblázatkezelővel számíttattam (50000 sorral), és kb 4,398*10^ -5j jött ki. Ettől nyilván kisebb jön ki helyes megoldásra.

Szia!
Szerintem a kondiba betöltött töltésmennyiségből kell kiindulni. Ha a kondi fesz 0 volt, akkor Q= C*U, jelen értékekkel: Q=2,2*10^-9 * 2*10^2= 4,4*10^-7 As. Az összes töltés 200V-on lett kivéve, ezért a tápból kivett energia E= UQ, jelen értékekkel: E= 8,8*10^-5 J. Az összes kivett energiának pont a fele ment a kondiba, 1/2Cu^2 = 1/2QU, illetve a másik fele elmelegedett az ellenálláson. A kérdezett hőenergia 4,4*10^-5 J, aminek nagysága az R értékétől független.

Ő...

Köszönöm, de nem vagyok benne biztos, hogy a "veszteség" független az ellenállástól!

Másképp morfondírozva: ha az ellenállás az "eredetihez" (47ohm) képest század akkora (tehát 0,47ohm), akkor a töltőáram kezdeti értéke és így minden pillanatértéke is éppen 100 szor akkora lesz. Ha minden kis pillanatban kiszámítjuk az ellenálláson folyó áramot (mondjuk kis dt momentumok, amikhez kis i -k tartoznak), és ezt a kis ideig tartó áramot négyzetre emeljük, majd szorozzuk az ellenállásával, akkor...

Ha már csak az első kis dt -t és hozzá tartozó áramot emeljük négyzetre, akkor látszik, hogy 100-szoros áramhoz már 10.000 szeres teljesítmény tartozik. Hiába 100-ad akkora a tau (tehát ez a teljesítmény az ellenállást az eredeti esethez képest század annyi ideig fűti), 10.000/100=100. Szóval 100szor kisebb ellenállás már 100szor nagyobbat fog disszipálni.

Ajjajj. Lehet, hogy igazad van, mert az ellenállásunk értéke (az I^2*R -ben) is 100-ad akkora.

Ez őrület

Most kiszámoltam az elved alapján:
C/2*U^2= 2,2nF/2 * 200V^2=
=0,000044= 4,4*10^ -5j energia jött ki egy feltöltésre.

A vicces az, hogy én kvázi kiintegráltam ezt a dolgot táblázatkezelővel, 50.000 kis részre bontottam az áram exponenciális görbéjét 5TAU ideig.

Ez jött ki: 4,398*10^ -5j. Tehát még is csak igazad lehet.
Köszönöm a segítséget!

Szia!
Megerősítésképpen én is kiszámítottam, pusztán matematikailag integrálással a 0-5*RC időtartományra. Én az ellenálláson eső feszültség alapján számítottam ki az energiát, az eredmény egyezik a Ti megoldásotokkal- nálam 4,39999*10^-5 J lett.

De ha integrálható volt (bevallom, lusta voltam még gondokkodni is rajta), akkor eleve mi volt a probléma?

Probléma nem volt, csak ezt kellett kiszámítani. A kérdező excel táblával téglány összegekkel, Peter65 energia megmaradás alapján, én meg a teljesítmény időfüggvényének integrálásával hoztam ki az eredményt. Ennyi.

Ugyanahhoz az (akár helyes) eredményhez többféle úton is el lehet jutni. Ezzel nincs semmi gond és nagyon dícséretes dolog