Fórum témák
» Több friss téma |
Fórum » Házi feladat elmélet - tételek
Sziasztok!
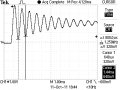
A következő házi feladatban kérném a segítségeteket: Adott egy soros RLC kör, aminek a ki/bekapcsolási tranziens jelenségeit vizsgáltam. Uo=4V DC feszültséget kapcsolgattam a körre, közben a szkóppal rögzítettem a kapott jelalakot. A mérőkörben adott volt az ellenállás: 27.4ohm és a kondenzátor: 47nF. Mindezekből kellene kiszámolnom a tekercs induktivitását. Az ábráról a periódusidő: 800us, a csillapodás 320mV. A tanár (hibás) diffegyenlet rendszert írt fel, nemigazán boldogulok ill boldogulunk a megoldással. Remélem valaki tud segíteni, hogy hogyanis kellene kiszámolni. Előre is köszönöm!
A periódusidőból és a kondiból, thomson képlettel számított induktivitás miért nem jó?
800us -> 1,25kHz L = 1 / ((2*Pi*F)^2 * C) = 344,9mH
A felsőoktatásban kell benne lennie differenciálnak, integrálnak vagy komplex számokkal való bűvészkedésnek hogy komolyabbnak látszódjon. Még ha ugyanaz is a végeredmény.
Hát, én középiskolában tanultam komlex számokat, differenciált és integrálszámítást is - akkor még nem volt érettségi tétel, de az elektró miatt mégis kellett.
Amúgy meg elővettewm a szimulátort, és a csillapodó rezgés miatt tényleg nem ad tök pontos eredményt a thomson képlet, (de amúgy igen jó közelítés).
A Thomson képlet amúgy tök pontos eredményt kell hogy adjon. A csillapodásban van szerepe az ellenállásnak. (Q)
A csillapodó rezgés már egy összetett jel (nem egyetlen frekvencia) ami felbontható több frekvenciaösszetevőre. Ennek a nullaátmeneteinek és/vagy a maximumainak az időbeni különbsége nem egyezik meg teljesen az alapharmonikus periódusidejével.
Köszönöm a segítséget, közben máshonnét is jöttek megoldás javaslatok, valahogy megpróbálom összehozni jól (bár hogy hogyan vezetem le az még kérdéses).
Biztos vagy benne, nem sok felharmónikus tartalma van annk a rezgésnek, mi lehet az oka?
Én csak olyasmire gondolnék, hogy a kisebb amplitúdó miatt a vasra kisebb gerjesztés kerül, így annak induktivitása változik (ur nem független a térerősségtől). Tehát a nagy amplitúdójú szakaszon mérve és abból számolva megfelelően pontos érték adódik.
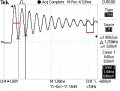
Sőtt grafikusan mérve nem változik észrevehetően a frekvencia.
A két piros vonal azonos hosszúságú!
Ez természetes, hiszen a rezgés frekvenciáját, ahogyan pucuka is írja az L és C elemek határozzák meg. Az R a csillapításért felelős, tehát az amplitúdó időbeli csökkenéséért. Gondolom ez egy valóságos kapcsolás, emiatt nem meglepő, hogy nem stimmel a számított és a szimulált eredmény, hiszen az alkatrészeknek van a gyártásból eredő szórása, illetve hőmérséklet függése is.
Valamint nem ideális alkatrészek, tehát kondi és tekrenc belső ellenállása, ellenállás induktivitása (ha spiráköszörlt v. huzal) is beleszól.
Konkrét mérést nem végeztem, de szimulátorba beledobáltam a soros RLC kört. Ebben is kimutatható, hogy a periódusidő kicsit hosszabb lesz mint ami a sima LC körből adódna, és ráadásul nem is ugyanannyi mindegyik periódusban!
Azonban az eltérés igen kicsi, de egy mérnöknek illik tudnia, hogy van eltérés, és hogy általában elhanyagolható mértékü (de nem mindíg, és nem minden esetben). Szerencsére nekem nem kell ilyesmiket számolgatni, de ha nagyon kellene, akkor inkább a gyakorlatban mérnék, vagy szimulátort használnék. (mindkettő hamarabb vezet eredményre mint a matekolás) Kíváncsi lennék, hogy a kérdező végülis mire jutott..?
Hidd el, hogy a periódus idő (frekvencia) nem változik a lecsengés alatt. Az annyi, amennyit kiszámolsz, már ha a helyes értékekkel számolsz. Nem tud más lenni, egy színusznak nincs felharmónikus tartalma, egy lineáris áramkörben mitől is lenne. Az ellenállás (ami többnyire a veszteségi ellenállást reprezentálja) a frekvenciát nem, csak az amplitúdót befolyásolja.
Azért a helyzet nem ilyen egyszerű, egy veszteséges rezgőkör rezonanciája eltér az ideálisétól.
Bővebben: Link Lsd. Ugrásfüggvény átvitel c. részt. Idézet: „egy színusznak nincs felharmónikus tartalma” Egy szinusznak nincs, de ez nem szinusz! Ha változik az amplitudó akkor már összetett jel, ami (Fourier szerint) szétbontható több szi9nuszos összetevőre. Idézet: „nincs felharmónikus tartalma, egy lineáris áramkörben mitől is lenne.” Pl. attól, hogy a bemenet egy impulzus (bekapcsolási tranziens) aminek ugye végtelen széles a spektruma. A rezgőkör ebből nagyjából kiszüri a saját frekijét, de mivel a jósága véges, marad több összetevő is. Ha végtelen lenne a jósági tényező akkor folyamatos szinusz lenne az eredmény. Idézet: „Feltűnô, hogy a rezgôkör jelenlétére jellemzô frekvencia - nullától különbözô R értékeknél - mindig kisebb, mint a Thomson frekvencia.” Ez lehet, pillanatnyilag nem látom át, de a magyarázat a linkelt anyagból elég meggyőző. De. Az R értéke a lecsengési folyamat alatt nem változik, mert értéke kiindulási feltétel volt, így a lecsengési folyamat alatt a frekvencia sem változik. A felharmonikus tartalom, meg teljességgel nem magyarázat. A jósági tényező sem vátozik a lecsengés alatt. Ésszerű a lengő tömeg hasonlat magyarázata.
Ez nem szinuszjel, hanem egy exponenciálisan lecsengő un. kváziperiodikus jel, aminek a spektruma egy végtelen sorozat.
A lecsengési folyamat alatt, a maximumhelyek távolsága vagyis a periódusidő állandó, ezt nem is vitatjuk, de ez nem egyezik meg az L és C elemekből a Thomson formulával számolható eredménnyel. Villamosságtan
Értem, és nem is vitatom.
A második részben ekkold felvetésére válaszoltam, hogy a sávszűrős megközelítés nem jó, és a periódus idő (frekvencia) az idővel nem változik a harmonikus tartalom miatt.
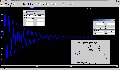
Csatolok egy képet: szimuláció Tina6-al. A lengés elején kicsit kisebb a periódusidő, mint a vége felé (802/828 usec). Akkor most a Tina hibás, vagy valami mégsem stimmel?
Nekem egy másik mechanikai hasonlat is eszembe jutott. Egy leesett ping-pong labda pattogása esetén hallható, hogy a pattogások nem álandó sürüségüek - bár itt a működés más, nem lehetséges , hogy van valami ami mégis okozhat periódusidő változást? Mondjuk a feladattól eltérően én a pozitív periódust kezdő nullaátmenetek távolságát vettem periódusidőnek (csak mert ez logikusabbnak tünt) - de gondolom nem ez az eltérés oka. Egy gondolat: talán a harmonikusok nem egyforma sebességgel csillapodnak, és ez okoz ilyesmit. Lehet, hogy a végén összedobok egy mérést valós alkatrészekkel ?.... 
Nekem LTspice4-el azonos periódusidőt szimulál.
A kondi feszültségét néztem. A png kiterjesztést valamiért nem csatolta normálisan.
Na ezt meg automata átméretezés érte.
Végsősoron a helyes megoldást az eltés jegyzet soros rezgőköröknél tárgyalt levezetése adta volna, a baj az volt, hogy a mérés során a tanárunk rosszul írta fel ezeket a képleteket, így nemtudott senki értelmesen számolni velük. A csillapodásból kellett volna alfát, a periódusidőből bétát számolni, bár hogy minként, az még tisztázatlan. Köszönet mindenkinek a segítségért!
Sziasztok!
Egy mérőbélyeges átalakító hogy néz ki illetve ennek hogy néz ki a mérőköre? Mi a kompenzálóbélyeg feladata? Az utolsó pedig,hogy mi a különbség az induktív és az indukciós átalakítók között?
Sziasztok!
Holnap fizika tesztet írunk, elég rosszul állok fizikából, ezért kéne egy kis prefixumos segítség!  Valaki kérem ellenőrizze ezt le !  Át kell váltani: a) 34560dm --> m b)789724 pg --> g c)559g--->dkg d)55,5cl-->dl e)8,91dkg-->kg f)3456mF-->kF Ja, és mellé kell írni a normál alakját is ! Kérem csak olyan írja le a választ rá, aki tényleg érti, van fizikai tudása, nem 8.-os, vagy hasonló, és ő is csak "elméletben" tudja, mint én..  A - valami az az index akar lenni, csak nem tudom lekicsinyíteni.. :- ) a) 34560 * 10-1 m ---> 3,456 * 10+3m b)789724 * 10-12g ---> 7,89724 *10-7g c)559 * 10-1dkg ---> 5,59 *10 +1dkg d)55,5 * 10-1 dl --->5,55 * 10+0=5,55dl e)8,91 * 10-2 kg ---> 8,91*10-2kg f)3456 * 10-6 kF ---> 3,456*10-3kF Üdv !
És nincs mese, be kell vágni. Ez is az alapok alapja.
Tudom, de nem lett jó? Nem ellenőrizné le valaki? Nekem sokat számítana.

Ha ez megnyugtat, akkor én nem találtam benne hibát.
Juj, köszönöm ! Ez megnyugtat. Nekünk amúgy a teráig, meg a pikoig kell tudni, és tudom én fejből is, csak ez - pontos feladat, nem akarom elbukni, főleg, hogy 4-est szeretnék.
 |
Bejelentkezés
Hirdetés |