Prímtényezőkre kell bontani, ami 5*19*31*103, és ebből a legvalószínűbb adat a 31 év

Látom ez túl könnyű volt Na akkor....

16. A rendőrfelügyelő és a matematikus nyomoz!
Egy fogadáson, száznál több, de kétszáznál kevesebb pohár vörösbor van előkészítve a vendégeknek,
és a rendőrfelügyelő szerint közülük egyetlenegy mérgezett.
Matematikusunknak a lehető legkevesebb méréssel kell megállapítania a helyszínen, egy
kis hordozható laboratórium segítségével, melyik a mérgezett bor. Egy mérésben több pohár tartalmá-
ból is lehet egy mintát összekutyulni, és a méregből egész kicsi dózis is kimutatható.
- Válasszon egy poharat, először azt mérjük egyedül! - szólt a matematikus a felügyelőhöz.
- De hát ez pazarlás, így biztosan több mérés kell majd, mint a minimum! - képedt el a felügyelő.
- Ugyan már, ne higgye, csak tegye nyugodtan, amit mondok! - mosolygott a matematikus. - Kü-
lönben is egy kis szerencsejáték jót tesz az emésztésnek.
A matematikus pontosan tudta, mit beszél, tehát pontosan hány pohár bor volt a fogadáson előkészítve?
Hány mérést kellett maximálisan végezni a laborban?

17. Van 6 doboznyi kondenzátor, mindegyik egyforma külsejű, és pontosan 100nF kapacitású. Azonban a 6 doboz között van 1 vagy több olyan, amelyben 100nF-os kondenzátorok helyett csupa 110nF-os kondi van. Meg kellene határozni, hogy melyik dobozban vannak 100nF-os és melyikben 110nF-os kondik, a lehető legkevesebb méréssel. (a kondik tetszlés szerint variálva összeköthetők a méréshez - pontos kapacitásmérőt használunk - és a kondikit is pontosnak feltételezzük, tehát nincsenek közbenső értékszórások)
Tehát legkevesebb hány méréssel lehet eldönteni a kérdést?
Milyen mérési elrendezést kellene használni?
-->És hogy ne tűnjön annyira egyszerűnek néhány mérésből megmondani az eredményt, ideírom, hogy EGYETLEN méréssel meghatározható, hogy melyik dobozban vannak 100nF-os és melyikben 110nF-os kondik, de vajon hogyan??<--

Üdv!
1 méréssel!

A dobozokat sorszámozzuk, és a sorszámnak megfelelő darabot veszünk ki belőle. Mind a 21 kondenzátort párhuzamosan kapcsoljuk. Az eredő kapacitás 10nF helyi-értéke a keresett doboz.
->Szerk.: 16.->129

És ha nem csak 1 dobozról van szó (egy vagy több)...?

Bocs, a "több" felett átsiklottam. Mértani sor szerint kell mintát venni.

Az első dobozból 32-őt, a másodikból 16-ot...a hatodikból egyet. Párhuzamos kapcsolásban végezzük el a mérést. Kivonással megállapítjuk az eredő kapacitás hányszor 10nF-dal több mint, ha minden kondenzátor 100nF-os lett volna. Eredményünket írjuk fel kettes számrendszerben hat karaktere. Amelyik helyi-értéken egyes szerepel, a neki megfelelő dobozban 110nF-os kondik vannak.

Nagyon leült ez a téma, pedig érdekes kérdések merültek fel!
Engem speciel nagyon érdekelne, hogy honnan jött ez a prímtényezős felbontás a hajókás kérdésnél!
A borkóstolós megoldása is várat még magára..

A tippem: 129
A folyamat valahogy úgy néz ki, hogy összekever a minták feléből (64 db) egy adagot, ha benne van a méreg, akkor azok közül is kiválaszt p/2-t vagyis 32-t, ha nincs, akkor a másik adagból választ 32-t és így tovább felezi az összekevert minták számát, amíg csak kettő marad, amiből már egyértelmű. És mivel több eggyel van mint 2^x (jelen esetben x=7) így éppen 1:129-hez az esélye, hogy a plusz pohárban lesz a méreg, de ha benne van, akkor kevesebb mérés kell, mintha végigmérné az összeset, és a végén derülne ki, hogy mégis a kiválasztott a mérgezett.
Ha már írtam akkor egy könnyű feladat.
Van egy szoba, benne 3 kapcsoló. Mindhárom kapcsoló egy másik szobában található villanykörtéhez tartozik, tehát 3 kapcsoló és három körte van. A kapcsolós szobából indulunk, ott először az összes kapcsoló le van kapcsolva, amiket tetszés szerint kapcsolgathatunk. Ezután átmegyünk a másik szobába, ahol meg kell állapítanunk, hogy melyik körte, melyik kapcsolóhoz tartozik. Az egyik szobából nem látunk át a másikba, nincs nálunk csavarhúzó, multiméter, stb., 3 egyforma kapcsoló, és 3 egyforma körte van egyforma vezetékekkel.

Sziasztok! Szerkesszetek 40 fokos szöget, csak körzőt és vonalzót szabad használni. Agytornára igen jó ez a feladat. Ha lehet ne utánanézzetek, hanem gondolkodjatok, sok sikert. Üdv.: Yoe

Ez tényleg gondolkodtató! Köszi.

Sikerült . Kb 15 perc volt... Ebből 10 ig körzőt 2 ig vonalzót kerestem
Annyit még hozzátennék, hogy csaltam ugyanis 2 vonalzót használtam illetve bátorkodtam elővenni egy ceruzát is

Szerintem: a kőr 1/9-ed része. Minél nagyobb kőrt rajzolunk, annál pontosabban osztható a kőrkerület (persze a kerületet kell kiszámítani).

Felesleges Ha "engedélyt kapok rá" felrakom a (szerintem) legegyszerűbb megoldást

Szerintem euklideszi szerkesztéssel nem lehet megoldani a feladatot. Van rá tétel, hogy melyek azok a szabályos sokszögek, amelyek szerkeszthetők. A kilencszög nincs közöttük. Ha 40°-os szöget lehetne szerkeszteni, akkor kilencszöget is lehetne szerkeszteni.

Hidd el, hogy meg lehet körzővel és vonalzóval szerkeszteni.
Senki nem mondta, hogy euklideszi módszerrel kell.

Nálam a szerkesztés az euklideszit jelenti

Ezt IV.-ben('58) Tóth tanár úr gyakoroltatta velünk. Körző, vonalzó, cerka.

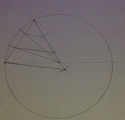
Én egy ilyen megoldásra jutottam. Amennyire látom/le tudom mérni ez pont 40 fok

Nem jó a megoldás, mert ceruzát is használtál!

Áááá. A válaszok tökéletesek. Igazándiból a kérdést kellene továbbvinnem, Én is így oldottam meg a kérdést: hogyan lehet ugyanígy 10 fokos szöget szerkeszteni (majd 20, 40, 50, 80-ast) szögmérő használata nélkül. Természetesen a ceruza megengedett .

Egyébként ezt Eukledeszi geometriának mondják (ennek azért véletlenül is, de rátaláltm, korábban nem is tudtam, hogy így hívják), Ők csak körzőt és vonalzót használtak. Egyébként a kérdést általános iskolában szokták feltenni.

Picit sántít, a középső és a szélső 20°-nak vélt csúcsszögű háromszögek nem fedik egymást. Van kék-két azonos hosszúságú oldaluk és a harmadik eltér.

Most olvasom az Eukledeszi módszert, hogy említetted. Egyébként meg lehet úgy is csinálni. Nekem sikerült, majd elmondom. Jó?

Mondhatod hogyan, kíváncsi vagyok rá Én csak annyit tudok, hogy a tétel szerint nem lehet megszerkeszteni, tovább nem foglalkoztam vele. Biztos meg lehet trükkökkel oldani, de az már nem euklideszi szerkesztés. Itt: Bővebben: Link az áll, hogy csak azok a szabályos n-szögek szerkeszthetők, ahol n 2 hatványának és különböző fermat prímeknek(ezek: 3; 5; 17; 257; 65537) a szorzata(a fermat prím helyett 1 is lehet a szorzatban). Így az első néhány szerkeszthető szabályos sokszög: háromszög, négyszög, ötszög, hatszög, nyolccszög, tízszög, tizenkétszög stb...
Ha 40 fokot lehetne szerkeszteni, akkor ebből 9-et egymásra szerkesztve "csillagszerűen" és egy kört szerkesztve a középpontból kijelölne 9 pontot amiket összekötve meg lenne a szabályos kilencszög. Dehát a tétel szerint nem lehet, ez van . Remélem nem untattam senkit

Kicsit részletesebben : Először is veszel egy kört, középpontból húzol egy tetszőleges irányú vonalat, erre 60°-ot, a 2 pontot összekötöd(nevezzük 60 as vonalnak).
Az egyik pontból(én a végpontból) húzol egy tetszőleges irányú vonalat, ésszerű +/- 30-90°-osat(az "összekötő" vonalhoz képest), de bármilyen lehet 0-án és 180-on kívül.
Erre a segédvonalra körzővel felmérsz 3 egyenlő távolságra lévő pontot, az utolsót összekötöd az alapvonal kezdőpontjával. Így kapsz egy háromszöget.
Ezt a lezáró vonalat párhuzamosan eltolod a másik két egyenlő távolságra lévő pontba. Ekkor kiadódik a a 60 as vonalon 2 pontod.
A kör közepéből ezen a 2 ponton keresztül húzol egy-egy vonalat, ami elmetszi a körívet.
Ezt leírni sokkal bonyolultabb mint megszerkeszteni . Úgyhogy egy kis folyamatábra szerű képsort felrakok.
Az utolsó képen látható eszközöket használtam. Illetve a párhuzamos eltoláshoz még 1 "vonalzót"

Eddig világos Belátható, hogy alfa és béta szögek nem lehetnek egyenlőek? Ha igen, akkor az összegük sem lehet 40°.

Pedig az asztalon nagyon egyenlőnek tűntek. De szerintem holnap ennek nekifutok megint. Ez valami szerkesztési hiba lesz.

Szia. A módszerem a következő: húztam egy vonalat, körzőnyílásba vettem egy szakaszt, bármekkorát, de nyilván valami értelmeset. Ezt 9-szer felvettem a vonalra, majd a két végpontból körzővel felvettem egy szögfelezőt, persze ezt nem kell behúzni, de metszéspontban pontosan 90 fok van. Ebből a pontból összekötöttem az előbb felvettek, és mint 90 osztva kilenccel: 10, 20, 30....90 fok. Szerintem ez is eukledeszi szerkesztés, mivel csak körzőt és vonalzót használtam. Kellemes vasárnapot.