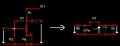Fórum témák
» Több friss téma |
Fórum » Házi feladat elmélet - tételek
2 micsoda? Egyébként nem tudom hány éves a kapitány, de neked kell kiszámolni. Csak annyit mondtam, hogy ha a dimenziók stimmelnek, kevesebb bajod lesz.
Végül is 2Tesla korrektnek tűnik.
Köszi a segítséget. Esetleg a Taus kérdésre nem tudsz valami megoldást? Közben agyaltam kicsit meg utána lestem itt-ott az Le/re tuti jó lesz, de mivel ugye az 5ns-hoz képesz az 50ns állandósult állapotnak minősül, az áramkörben ekkor folyó áram U/Re. 5v/2kOhm=2,5mA. Lehet ez jó megoldás?
De nem jó.
A mágneses fluxus mértékegysége nem Tesla. A 2cm az meg nem a kör területe. Előbb számold ki az indukciót (ehhez kell a kör területe..), aztán ebből a fluxust.
Jaa!
Na akkor tisztázás végett, hogy negyedjére esetleg jó legyen. a Fluxushoz: a kör területe 2*r*pí tehát 2cm*pí= 6,283cm^2 Most kell az indukció (B?) ami szerintem uo*ur*H A H pedig a térerősség, ami esetünkben 100A/m volt Így megfelelő, vagy még mindig tovább kellene gondoljam?
Előzőt szerkeszteni már nem tudtam, úgyhogy ide írom:
Kiszámoltam, hogy A=2cm*pí, tehát 6,283cm^2, ami 0,0628m^2. A B=u0*ur*H=100*1,257*10^-6*400= 50,28*10^-3 Am/m A fluxus pedig B*A tehát 50,28*10^-3 * 0,0628m^2= 5,028 Wb Így jó lesz?
Idézet: „a kör területe 2*r*pí” Húha! A B az rendben van szerintem, szorozd be a rendes területtel (a m^2 és a cm^2 között nem 100 a váltószám) és kész
Vegyél elő egy függvénytáblázatot. A kör területe egyébként R[sup]2[/sub]*pí
Igazad van!
Akkor most újragondolva! A=3,14cm^2 ami 0,0314m^2 B=50,28*10^-3 Am/m Fluxus pedig 50,28*10^-3 * 0,000314Am/m = 15,787*10^-6 Wb Jó nem jó? "nem 100 a váltószám" Akkor még mindig átgondolom... Közben javítottam
Még mindig nem 100 a váltószám m^2 és a cm^2 között.
1m*1m=100cm*100cm
Ha már indításkor átszámolod az értékeket abba dimenzióba, amit már használsz, sokkal kisebb a tévedés esélye. Akár normál alakban is, és akkor nem kell az átváltással bíbelődni, csak a számítások elején, és végén, akkor is, csak ha szükséges.
Javítottam, előzőben.
A következő problémám szintén torroidos feladattal kapcsolatban van. Egy légréses torroid tekercs légrésében a térerősség 80kA/m. mekkora a térerősség a vasmagban, ha a ur=200, Mekkora a fluxus, ha a vasmag 2cm átmérőjű kör keresztmetszetű. Annyira jutottam vele egymagam, hogy Blevegő=80kA/m És kell a Bvas, amit úgy tudok kiszámítani, hogy u0*ur*H De a H-t nem tudom kiszámolni úgy, hogy ne legyen benne itt ismeretlen. H=B/u0*ur ; vagy gerjesztés/lk; más variációt nem találtam most rá . Ezt hogy kell? --- Vagy az jó, hogy Hl= B/uo tehát 80kA/1.257*10^-6 És ez a H használható a Bvashoz?
Ez ugyanaz a feladat, csak most a légrésben van megadva a térerősség. A magban a térerősség ur-ed része lesz, a többi teljesen ugyanaz.
Rendben, akkor megoldom, utána meglesem a többit is, hátha megy valami, de majd még jelentkezem.
Köszönöm a segítséget mindkettőtöknek!
Na azt hiszem megoldottam.
Hvas=80kA/m / 200 = 400A/m A= 3,14 cm^2 tehát 0,000314m^2 Bvas=H*u0*ur = 100,56*10^-3 Fluxus= B*A= 31,575*10^-6 Wb Remélem ez így jó. De ezek a tekercses dolgok eléggé nehézkesen mennek nekem. Itt van mindjárt a következő, ami most négyzetes alakú vasmaggal szól. Szóval: Egy 4cm^2 négyzetes keresztmetszetű V360-50A trafó lemezből készült vasmagban 1mm-es légrés található. A vasmag térerőssége 100A/m. A vasmag külső méretei 100mm*100mm. Mekkora lesz a légrésben a fluxus ha az 1000 menetes tekercset 232mA gerjesztő árammal tápláljuk? Gyanítom itt teljesen más képletek érvényesek, mint az előzőnél. Vagy nem?
Közben megoldottam még egy feladatot is, ami így hangzik:
Egy 500menetes 1650 relatív permeabilitású vasmagos tekercs hossza 4cm, átmérője 1cm, Mekkora a gerjesztés, a mágneses térerősség, az indukció és a fluxus, ha a tekercsben 2mA áram folyik? Így oldottam meg: Gerjesztés I*N =1Am Térerősség H=gerjesztés/lk ahol lk a 4cm méterbe behelyettesítettem... = 25Am B=u0*ur*H =51.85*10^-3 Am fluxus=B*A 0,5^2cm*pí = 0,0000785m^2 * 51,85*10^-3 = 4,049*10^-6 Wb Nem tudom ez így megfelel-e a valóságnak, vagy sem!?
Szerintem ez akkor lenne így jó, ha a vasmag egy 4cm középkerületű toroid lenne. A feladat olyan tekercsről szól az értelmezésem szerint, amiben 4cm hosszú egyenes vasmag van. Ha felrajzoljuk a fluxus útját, belátható, hogy a 4cm vason kívül legalább ennyit a vason kívül halad. A vas magas permeabilitása miatt a mágneses térerőssége zöme leginkább a vason kívül esik. Számolni valahogy így kellene:
Gerjesztés=(B/u0)*l(vason kívül)+(B/u0*ur)*l(vas, azaz 4cm) l(vason kívül) értékét csak közelítőleg lehet szerintem meghatározni, ráadásul ez azért eléggé inhomogén tér. Talán nem követsz el nagy hibát ha mondjuk 6cm-nek tekinted. Ha B megvan, akkor a többit már ebből ki tudod számolni.
Értem, de így a B sincs meg.
Ugyanis B= u0*ur*H val számoltam, viszont a Hhoz meg gerjesztés/lk képletet alkalmaztam, tehát egyik következik a másikból. Sehogy sem jó ez így. akkor a H-t kellene meghatározni máshogy. De miből?
A korábban felírt egyenletben csak egy ismeretlen van, a B. Előbb ezt számolod ki, és ebből a H(vason kívül) és a H(vas) értékét.
Norberto!
Nagyon köszönöm a segítségedet!! Boldog Új Évet kívánok! Bocs a késői reagálásért. Üdv. Bosch
Sziasztok. Esetleg tudna nekem valaki nagyon gyorsan segíteni? Csatoltam a feladatot. Valaki elmagyarázná nekem érthetően az ilyen és hasonló kapcsolások megoldását? Az alapokkal tisztában vagyok, az egyszerű alapkapcsolások mennek is, de ebbe nagyon belebonyolodtam. Az Au-t kell kiszámolni.
Köszönöm szépen.
Szia!
Valószínűleg a rajzon a kimenetnél lemaradt egy kötést jelző pont. Én úgy vetem, mintha ott lenne. Ha közben rajzolgathatnék, talán könnyebben lenne, mint csak így szavakkal kifejezni. A kapcsolásban kettő feszültség adott, az Uin és az Uout. Még egy feszültséget érdemes felvenni, a műveleti erősítő bemeneteinek feszültségét (legyen Um). Ezen feszültségekkel kifejezed az egyes ellenállásokon folyó áramot. A rajzból adódóan Ir1 és az Ir2 megegyezik, ezért a két kifejezésből felírható egy egyenlet. Az Ir5=Ir3+Ir4, ez alapján felírsz még egy egyenletet. Kettő egyenleted van három ismeretlennel (Uin, Uout, Um). A két egyenletből kiejteted Um, így marad egy egyenleted kettő ismeretlennel (Uin, Uout). Kifejezed a kettőjük arányát, ami ugye az erősítés. Nekem elég cifra eredmény született: Au=(-R3R5(R1-R2)+R3R4R2+R1R5(R3+R4)) / (R4R5(R1-R2)+R3R4R2+R2R5(R3+R4)) Lehet hogy van egyszerűbb megoldás is, én ezt az utat ismerem.
Szia.
Köszönöm a megoldást, valószinűleg helyes is. Mi itt felvidéken eléggé érdekes módszereket tanulunk. Csatoltam egy mintafeladatot, ha érdekel nézd meg. A bemeneti ellenállást kell kiszámolni. 3 féle módszerrel van. Sajnos nemtudom a magyar megfelelőit, csak az egyiknek, virtuális 0, vagy földpont lehet. Azt mondta az egyik prof., hogy elég ha a virtuális földpontosat tudjuk, a többit ugyis elfelejtjük. Nemtévedett sokat.Elfelejtettem mire hazaértem.
Talán a b) megoldás felel meg annak, ahogy számoltam. A mátrixos megoldást nem ismerem, de lehet, hogy egyes esetekben hatékony lehet.
A következő feladat csúnyán megszivatott vizsgán. Egyedül az utolsó kérdést tudtam megfejteni a könyv által. Esetleg valaki tudja a másik kettőt? Lehetőleg a jövő hét közepéig kellene a megfejtés.
Egy oszcilloszkóp képernyőjén az alábbi ábra látható. A bemenet kapcsolója DC, a bemeneti osztó 50 mV/div, az időalap generátor 0.2 ms/div állásban van. A jelet három különböző elven működő műszerrel is mérjük váltakozó feszültségmérő üzemmódban. (ld. kép). 1. Mit mér és mit mutat a 2Ü átlagérték egyenirányítós Deprez műszerrel rendelkező elektronikus műszer? 2. Mit mér és mit mutat a csúcsértékmérő egyenirányítóval rendelkező elektronikus műszer? 3. Mit mér és mit mutat egy true RMS rendszerű digitális mérőműszer? Umutat=Umér=Ueff=Ucs/gyök3=150mV/gyök3 Már az is segítene, hogy melyik mit mér és mit mutat, abból már rájövök, hogy kell kiszámolni. Előre is köszi!
Hali!
Egy tranyós alapkapcsolásos kérdéssel fordulnék hozzátok ezúttal. (kapcsolást sprintben rajzoltam meg mert más célprogramom momentán nincs) A kapcsolásból felírtam a bemeneti ellenállás, illetve a kimeneti ellenállás képletét, de nem nagyon sikerül a feszültség és áram erősítés képlete. Rbe= R2xh11e x[R1+(1/h22exRc)] Rki= Rcx1/h22ex [R1+(h11exR2)] Szerintem így alakul a dolog, de ha nem szóljatok! Az erősítésekkel viszont nem boldogultam. Ötletek?
A közös emitteres alapkapcsolásban az R1 jelű munkapont beállító ellenállás a bázis és a +Ut (ami váltakozó áramú sempontból GND) között van így az
Rbe = R1 x R2 x h11e Rki = Rc x (1 / h22e) levezetni nem akarom de Au = h21e ((1/h22e x Rt) / h11e) Ai = h21e ((Rt x Rc) / Rt)
Sajnos az R1 az negatív visszacsatolás is ezért az erősítések, meg a kimeneti ellenállás sem független tőle.
(Szerintem (meg a könyvem szerint))
Ezek a képletek esetemben nem jók, meg amúgy sem... Mert a terheletlen erősítés (-h21e/h11e)*[(1/h22e)xRc]
De esetemben az R1 söntöli a h11e-t és módosítja a h21e*iB-t. Szerintem kellene egy áramosztást számolni a fesz. erősítéshez ott, ahol bekapcsolódik a h21e*iB-be az R1 De ehhez segítségre lenne szükségem.
Sziasztok!
Adott egy párhuzamos RC tag. Jól számoltam, hogy az eredő impedancia ~ 98.2ohm? Köszi! |
Bejelentkezés
Hirdetés |