Csak egy kis elírás van benne: 3/7 *x + 5 = x/2 azaz 6 / 14 * x + 5 = 7 / 14 * x, azaz 5 = x / 14, azaz x = 14 * 5 = 70.

3. Magyarázat:
A p nem lehet 0, hiszen akkor a p*(x-1) függvény mindig 0, és nem veheti fel a +1 ..+3 értéket sehol sem.
Az (x+2) függvény értéke nagyobb 0 -nál a [-1 .. +1] tarományban. A p(x-1) p > 0 esetén csak a (+1.. +végtelen) intervallumban nagyobb 0 -nál. Tehát p < 0.
Ábrázold grafikonon a y1 = x+2 függvényt! Most itt eltekintek tőle, elég annyi, hogy x = -1 -nél y1 = 1, x = 0 -nál y1 = 2, x = 1 -nél y1 = 3.
Amennyiben p < 0, akkor az y2 függvény egy "lejtő", ami az x = 1 pontban 0 értékű. Annak az egyenesnek a p*(x-1) alakú egyenlete, ami átmegy a -1,1 ponton -0.5*(x-1). Ez pontosan a x = -1 pontban metszi a x+2 egyenest. Ha p ennál nagyobb, akkor a metszéspont x < -1 értéknél lesz. A p*(x-1) alakú függvény az x = +1 értéknél mindig 0, így itt nem lehet metszéspont. Ha a függvény "egy kicsit kevésbé lejt, mint a függőleges", akkor lesz metszéspont a x = -1 és x = +1 között.
Tehát: - végtelen < p <= -0.5.

Hello!
Újabb segítséget szeretnék kérni!
Előre is köszönöm!
Zsolt

Ezeknek a feladatoknak mi köze van egy elektronikai fórumhoz?

Ez nem elektronikai fórum hanem Házi feladat elmélet - tételek fórum!

Szerintem az, az egész oldal webcíme is utal rá. A topiknak valóban félrevezető a címe. Ha megnézed a topik legelső hozzászólást, akkor ott , igenis elektronikával kapcsolatos feladattal kapcsolatban kértek segítséget. Azóta véleményem szerint sok olyan feladat jelent meg itt a topikban , aminek semmi köze nincs az elektronikához, nem csak a te feladataidról van szó. Tudom, hogy aki tudod az szívesen segít. A többiknek nem tudom mi a véleménye róla , de én úgy gondolom túl sok a matematikai feladat ebben a topikban.

De amúgy ezeket a feladatokat megpróbálod magad megoldani, vagy csak posztolgatod a házidat ide? Mert azért egyik sem ördöngős, annyira legalábbis nem, hogy el se tudd kezdeni! Meddig jutottál, hol akadtál el? Egy kis (túl sok?) segítség alább. Remélem, nem néztem el semmit.

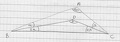
1. Abból indulj ki, hogy egy (ab) alakú kétjegyű szám felírható úgy, hogy 10*a+b, ahol 1<=a<=9 és 0<=b<=9 egész számok. A számjegyeinek szorzata a*b, összege a+b. Ebből egy nagyon egyszerű egyenletet kapsz.

2. 10*260+8*210+1000=5280 dínárt akar kapni összesen. A szilvalekvár tömege (10*3/4+8*2/3)*3/7=5.5 kg lesz. Innen már remélem, megy.

3. A teljes négyzet (x+k*p)^2 alakú. Ezt bontsd ki, és hasonlítsd össze az együtthatókat a feladatban megadottakkal. Például p=-7/5 esetén a kifejezés (x+6.2)^2 alakú lesz. Vizsgáld meg, hogy van-e még más megoldás is!

4. Ezt csak le kell rajzolni, és tudni, hogy mennyi egy háromszög belső szögeinek összege. Legyen az ABD=a és ACD=b, a keresett szög pedig BDC=c. Ekkor azt tudod felírni az eredeti háromszögre, hogy 120+3*a+3*b=180, a D pont berajzolásával keletkezett kis háromszögre pedig hogy 2*a+2*b+c=180. Ebből c rögtön adódik.

Köszönöm!
A 2.-at értem!
1.-nél leírnád az egyenletet?
3.-nál nem értem mit kell!
a 4.-nél pedig tudnál egy rajzott csinálni?
Ellőre is köszönöm!
Zsolt

Elég sürgős lenne!
Kérem segítsetek!

!? !? Mi ebben az a nagy nehézség???
2: 10 * a + b = a * b + a + b --> 10 * a = a * (b + 1) --> 9 = b... --> 19, 29, .. 99.

Kell holnapra a suliba, vagy mi? Szerinted ez korrekt dolog, hogy más írja meg a te feladatodat?

Azért mert nem értem és a tanár nem magyaráza el!
De ezen a 4 példán kívül a többit értem!
Szóval csak ezt a 4 példát magyarázatok el légyszi!
Előre is köszönöm!
Zsolt

1. Hp41C leírta.

2. Én leírtam.

3. (x+k*p)^2=x^2+2*k*p*x+k^2*p^2.
A feladatban: x^2+(4-6*p)*x+(9*p^2-7*p+11)
Össze kell hasonlítani a két kifejezésben x együtthatóját (2*k*p=4-6*p) és a konstans tagot (k^2*p^2=9*p^2-7*p+11), ebből egyenletrendszert kapsz k-ra és p-re.

4. Csatoltam.

A 3-ast még mindig nem értem!
Milyen egyenletrendszert?
A 4-esnél pedig egyenletet kapunk?
Milyen egyenletet?
Zsolt

Köszi!
De a 3 pont ahol van oda mit kell írni?
Zsolt

Olvasd el még egyszer a feladat szövegét! Számold ki, hány olyan szám van, ami teljesíti mindkét feltételt! Állapítsd meg hány kétjegyű, tízes számrendeszerbeli pozitív egész szám van! Innen már csak egy törtet kell felírni.
A három pont helyén kellene törni a fejecskét....

Sziasztok valaki tudna segíteni házi feladatban? Egy tranzisztoros közös emitteres erősítő kimeneti és bemeneti impedanciáját kellene grafikonban ábrázolni a frekvencia függvényében. A bemeneti impedancia még viszonylag egyértelmű de a kimeneti impedanciát nem tudom hogyan kell mérni.

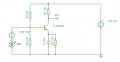
Papíron számítani vagy szoftverrel szimulálni kell? Elméleti számításnál a kimeneti impedanciát úgy definiáljuk, hogy 0 bemeneti feszültség mellett egy Ux feszültséget teszünk a kimenetre, és megnézzük, mekkora Ix áram folyik ennek hatására, Rki=Ux/Ix. Itt láthatsz rá egy példát (3/d feladat). Esetedben csak annyival lesz bonyolultabb, hogy nem csak valós ellenállások lesznek a helyettesítőképben.

Ha szimulálni kell, akkor is alkalmazható ez a módszer, csak okosan kell megválasztani a források DC szintjét, hogy a munkapontot ne bántsák, pl. a kimenetre tett forrást érdemes ideális áramgenerátornak választani.

De nem tudom!
Kèrlek segits!
Zsolt

Hello
Még csak a 4. feladatot nem értem segítenétek?

Ajajajajj!
Jelölje a C pontból az AB oldalegyenesre húzott merőleges és az AB oldalegyenes metszéspontját Q.
Ha FR szakasz hossza r, akkor a AQ szakasz hossza is r, azaz 895.
Ha DP szakasz hossza p, akkor a BQ szakasz hossza is p, azaz 1088.
Akkor az AB szakasz hossza p+r = 1983.
Segítségül hívjuk a jó öreg Pitagoraszt: (AB)^2 = (AC)^2 + (BC)^2.
Azaz: (AC)^2 + (BC)^2 = 1983^2 = 3932289.

Köszi de ez amit te leírtál ez az első feladat sor volt!
Azóta kértem másikhoz is segítséget!
Üdv!

Sziasztok. Segítséget köszönöm.
Fiam házi feladata, egyszerüsíteni kell a törteket. Belesültünk. Elég lenne, csak a levezetés, abból megértjük (talán) magyarázat nem szükséges.

(3x+1/21-9x)+(x+2/3x-7)-(x+1/6x-14) megoldás: -(1/6)

(x+1/x+2)+(2x-3/2-x)+(x^2 +2x+4/x^2 -4) megoldás: 8/((x+2)szorzásjel(x-2))

Ez hogyan értendő: (x+1/x+2) ?
1 : X + (1/x) +2
2 : (x+1)/(x+2)
Valamint a többi ilyen jellegű résznél ugyanez a problémám...

Úgy látom rosszul van zárójelezve, legalábbis az első.
((3x+1)/(21-9x)) + ((x+2)/(3x-7)) - ((x+1)/(6x-14)) =
(1/3)*((3x+1)/(7-3x)) + ((x+2)/(3x-7) -(1/2)*((x+1)/(3x-7)) =
( x + (1/3) - x - 2 + (x/2) + (1/2)) / (7-3x) =
(((x/2)-(7/6))/(7-3x)) = -(1/6) * (3x-7)/(3x-7) = -(1/6)

Az első feladat.
Ha kell a második is , akkor azt is megcsinálom. Remélem olvasható.

_{Nem a jó matekos hírében állok amúgy...}

Ha jól számoltam:
((x+1)/(x+2))+((2x-3)/(2-x))+((x^2+2x-4)/(x^2-4))=
((x-1)*(x-2))/((x+2)*(x-2))-((x+2)*(2x-3))/((x+2)*(x-2)) + (x^2+2x-4)/((x+2)*(x-2))=
((x^2 -2x+x-2) - (2x^2 + 4x-3x-6) + (x^2+2x-4))/((x+2)*(x-2)) = 0
Hatványokra
x^2: x^2 - 2x^2+x^2 = 0
x: -2x+x-4x+3x+2x = 0
konstans: -2 +6 -4 = 0

Hp41C
janikukac
Bocs, hogy rosszul, nehezen értelmezhetően írtam, de azt is sikeresen megfejtettétek, nem csak a matekot. Jobb lett volna ha fényképezem, nem gondoltam erre.
Köszönöm.

Volna még példa mellékletben -M18.jpg-, egyszerűsíteni kellene.
Annyit tudunk, hogy számlálókban nevezetes azonosságra alakítható: (a+b)^2 .
Most már megy a téma, csak ez az egy megállított.
Köszönöm a segítséget.

((a+b)*(a-b) + (a+b)^2) / (a-b) * ((a+b)*(a-b) / ((a+b)*(a+b))) =
((a+b)*(a-b) + (a+b)^2) / (a-b) * ((a-b) / ((a+b))) =
((a+b)*(a-b) + (a+b)^2) / (a+b) =
((a+b)*(a-b) + (a+b)*(a+b)) / (a+b) =
((a-b) + (a+b)) = 2*a