Fórum témák
» Több friss téma |
A mellékelt tábla nem jó. A táblák számozása és a C,D oszlopok elhelyezése se jó. A helyes elrendezés az általam küldött excel táblában a jó. A Karnaugh táblában a termek számozása az fix. Az excel táblában az alsó táblázatban, gray kódban elszámol decimálisan 15-ig. Ez a kód alapján van kitöltve a Karnaugh tábla. A termek jobb sarkába írt szám vízszintes és függőleges kódolással megegyezik a decimális értékkel. A betűk elhelyezekedése attól függ, hogy hányas helyi értéken foglal helyet. pl.: "ABCD" akkor a "D" az 1-es az "A" a nyolcas. Ha eddig tiszta akkor írj és írom tovább.
Nem hinném, hogy nem jó hiszen a jegyzetönkből vettem ki. Feltételezem, hogy egy Egyetemen ekkora hibát nem követ el egy tanár.
Akkor passzolom a dolgot. Olyannal még nem találkoztam.
Maradva az általad küldött excel-ben látható példánál:
F(1,2,4,5,6,9,10,13,14) Megrajzoltam a mellékletben és bejelöltem a termeket. A gondom, hogy a 4. pozíciónál a mintermet hogyan hozzan össze? Piros szerint vagy rózsaszín szerint? Én úgy vélem, hogy mindkettő kell. De, ha igen miért?
A piros hurkot én nem venném be, mert mind két hurokban szerepelnek.
De te miért nem vennéd bele?
Annélkül, hogy valósul meg a kapcsolat az összes minterm nélkül?
Elküldenéd - feltöltenéd a feladat eredeti szövegét?
Nincs konkrét feladat csak próbálom megérteni a dolgot. De úgy gondolom ez elég konrét: F(1,2,4,5,6,9,10,13,14)
Mi kell még hozzá?
A legelső hozzászólásban volt feladat, meg képlet is.
Azt szerettem volna látni, az azóta történt excel táblázást én se értem annyira. A De Morgan formulák segíthetnek.
Ilyen egyszerű feladatot kár bonyolítani De Morgan azonossággal. (szerintem)
Nem lenne semmi bajom, ha nem kellene vizsgáznom ebből. Eddig nem ismertem és nem volt szükségem a Karnaught táblára. 8 bemenetes logikai hálózatot megoldottam egyszerű igazság táblával. Ezzel a táblával még a 3-4 bemenetet sem látom át. Lehet bennem van a hiba, de ez egyenlőre csak bonyolítja az életem. Ha nem kellen K táblát használni az excel-es feladat nem is lenne kédrés, de a többi sem. [off] Egyébként meg ilyen feltételeket sokkal egyszerűbb leprogramozni és egy darab MCU-val megvalósítani számomra mint K táblákkal bajlódni.
Mint már írtam azért nem tenném bele mert már szerepelnek egy-egy hurokban nem az a cél (legalábbis ahogyan nekem tanították) hogy minél több hurok legyen hanem az, hogy minél nagyobb legyen a hurok. A kapcsolat az így is úgy is megvan köztük. A Karnaugh-nál a hurkokban lévők közt "ÉS" kapcsolat van a hurkok közt pedig "VAGY" kapcsolat van. Ezt akkor látod igazán amikor egyszerűsíted a hurkokat.
Itt egy példa. Látható a súlyozás. Egyszerűsítetlen alak és az egyszerűsítés.
Részben igazad is van, ha nem szempont a hazárdmentes kimenet. Ha nincsenek legalább egy közös hurokban az egy Hamming távolságra levő bemeneti kombinációk, akkor statikus hazárd léphet fel. Szóval a statikus hazárdtól mentes kimenethez kell a rózsaszínű és piros hurok is! Bővebben: Link
Ennyire hülye nem lehetek vagy rossz vonalat eröltetek.
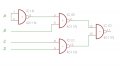
A feladat: Nem teljesen specifikált hálózat: 1 = 3,4,6,15 ; nem számít: 5,7,11 Most már értem, hogy: |AB+CD A feladat az lenne, hogy rajzoljam meg minimális számú NAND kapukkal. Ha megfeszülök sem sikerül. Segítsetek!
Köszönöm. Először ezt rajzoltam én is, de nem értem, hogy miért jó. Karnaugh táblát mellékeltem.
Csak az egyik fennakadásom: 4-re H szint kellene, de a kapcsolás alapján L szint lesz. 4 = 0100 |A és B rendben van ez ugye (01) ami 1. NAND kimenetén (1). CD itt negált (00) a 2. NAND kimenete szintén (1). Jön az utolsó NAND ami megkapja az (11) bemenetet, de a végleges kimenet így 0 lesz! Mit csinálok akkor rosszul?
"Mit csinálok akkor rosszul?"
Ezt: "|A és B rendben van ez ugye (01) ami 1. NAND kimenetén (1)." Az A kapu sima inverter, az 1,2 bemenetén lévő 0-ból a 3-as kimenetén 1 lesz. A B kapu bemenetére (5) kerül ez a jel, a másik bemenetére pedig szintén 1 kerül. Ekkor a B kapu kimenetén (4) 0 lesz. Ezután már a többi nem is érdekes, mert a D kapu kimenete csak akkor lehetne 0, ha mindkét bemenete 1 lenne, így viszont a kimenete 1 lesz.
Akkor lehet rosszul rajzoltam valami délután tina-ban ismét kipróbálom.
És hogyan nézne ki a dolog, ha AND kapukat kellett volna használni? Valahogy még nem látom át a K táblában, hogy mi-micsoda.
Végül is megértettem. Lazán elnéztem az inverter felett.
Próbálkoztam egy másik feladattal ahol ismét megakadtam  Teljesen specifikált hálózat NAND kauval. 1 = (8,10,12,13,14,15) Végeredmény: F=AB+A|D Ott akadtam meg, hogy hova kell ilyenkor kötni a (C) bemenetet?
Ha jó a végeredmény , akkor sehova. Hiszen az egyszerűsítés miatt kiesik.
Én is így gondoltam, de béna vagyok. Az állításod alátámasztod egy kapcsolásal?
A gond az , hogy nem NAND alakot adtál meg. Ezt még át kell alakítani.
Igen lehet. Pont erre keresem a megoldást. Én eddig úgy látom, hogy K tábla alapból NAND realizációt ad. De miből látod, hogy NAND alak vagy hogyan adok meg más alakot?
Azt miből gondolod , hogy alapból NAND relációt ad? A NAND alak , olyan logikai hálózatot valósít meg , amelyben csak NAND kapukat használunk. A K tábla egyszerűsítése után klasszikus kapuhálózattal megvalósítható logikai függvényt kapunk , mert a logikai összeadás, szorzás, negáció valamelyike szerepel a kiolvasott függvényben. Ha NAND alakban szeretnék felírni , akkor az kiolvasott függvényt még kétszer negálnunk kell. Így ebben , már csak NAND kapuk szerepelnek.
Amit megadott, azt minden átalakítás nélkül fel lehet írni NAND kapukkal, mert megfelel a szabályoknak.
Szabályok: -páratlan szinteken VAGY kapcsolatnak -páros szinteken ÉS kapcsolatnak -páros szinteken "bejövő" változóknak ponáltan -páratlan szinteken "bejövő" változóknak negáltan kell szerepelniük. Ha nem úgy jönnek be a változók, ahogy a szabály előírja, akkor a változót negálni kell. Ugyanilyen módok tisztán NOR kapukkal is meg lehet valósítani bármilyen függvényt, csak ott -páratlan szinteken ÉS kapcsolatnak -páros szinteken VAGY kapcsolatnak kell lennie A bejövő változókra ugyanaz a szabály. Szintekre példa: F1=A*B+C*D F2=(A*B*C)+(!A*D)+(B*!D) első szint=piros második szint=kék A első szint(ek) az a művelet(ek), amit legutoljára kell elvégezni. Második szint(ek) az a művelet(ek) amit utolsó előttiként kell elvégezni. Így tovább, az utolsó szint az a művelet, amit először kell elvégezni. A második függvényben a zárójeleket csak könnyítésként írtam, zárójelek nélkül is ugyanaz a függvény, ugyanolyan a műveleti sorrend. Ezek a szabályok nagyon szépen megvannak Szűcs László: Digitális áramkörök című könyvében, természetesen a levezetésekkel együtt.
De azért nem írtam rosszat, így is meglehet csinálni. Jól gondolom?
Nem látok benne hibát, jónak tűnik, a De-Morgan azonosságokat használtad, így jött ki a kinézésre is NAND .
Amit írtam, azért célszerű, mert a szabályok ismeretével, gyorsan, mechanikusan realizálható bármilyen nagy függvény, nem kell semmit átalakítgatni. Átalakításokat akkor kell csinálni, ha "szigorítva" van a példa, és kizárólag két bemenetű NAND kapukkal kell megoldani a realizálást.
Én még eddig csak "szigorított" példákkal találkoztam , ahol csak két bemenetű NAND logikai kapukat lehetett használni NAND átalakításkor. Ezért gondoltam azt , hogy csak így lehet megoldani.

Sziasztok!
Elvagyok a témával és néha értem is, de megint elakadtam. Volt egy feladat ahol F(1,3,9) Ez ugye: |B*D*|A+|B*D*|C Ezt meg is oldottam, de tök lett. Miért? Mert nem olvastam el a feladatot figyelmesen. Kizárólag 2 bementetű NAND kapu használható. Itt elvéreztem. Hogyan kell ezt levezetni? |
Bejelentkezés
Hirdetés |
A használat feltételei
• Adatvédelem
• GY.I.K., Használati útmutató és szabályok
• Impresszum
• Elosztó
• Hiba jelentése
K�rlek v�rj...