Fórum témák
» Több friss téma |
Fórum » Házi feladat elmélet - tételek
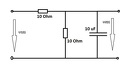
u1 -> rajzon jelölve, a bemeneti feszültség.
u2 -> a "kimeneti" feszültség (mondjuk a kondi 2 oldalán mérve) u0 -> semmi egyéb infó nincs róla, hogy hol van, csak annyi, hogy 1 V az értéke.
Ha az eddigi kapcsolás nem lett volna érthető, megpróbálom "cizellálni" kicsit: :p
(remélem így már nem kérdéses, hogy mi micsoda.  ) )
Nekem ez jött ki megoldásnak: u2(t)=0,5-0,5*exp(-20000*t) (ha a C nem volt t=0-kor feltöltődve)
Írjál fel egy csomóponti törvényt, abból kijön egy differenciálegyenlet és azt kell megoldani.
Valahogy így néz ki a grafikonja u2(t)-nek. A settling time most az időállandót jelenti.
Nem vagyok benne biztos, hogy ezt így kellene megoldani. Iskolai feladat lenne a cucc, ott nem szoktak ilyen nagy számokkal dobálózni.
Másrészt nekem nem a megoldás a lényeges, hanem az, hogy lépésenként hogy kell egy ilyen feladatot megoldani. :S
Ha felsőfokú intézményben adták fel a feladatot, akkor így kell megoldani. (általános megoldás) Ha nem, akkor adott peremfeltételek esetén megoldható diff egyenlet nélkül is, de ilyen adatokat nem láttunk.
Ettől függetlenül továbbra sem tudom a megoldás lépéseit...
Leírtam, remélem olvasható...
Bár azt még mindig furcsának találom, hogy a füzetben egy feladat sincs, aminek akár csak hasonló lenne a megoldása. A legtöbb ilyen u2(t) meghatározós feladatnak a megoldása olyan formában van, hogy:
u2(t) = x + y sin (omega t) ahol x és y AC és DC feszültségek. Idézet: „ahol x és y AC és DC feszültségek.” Elég szerencsétlen dolog ilyen elnevezéseket használni. Idézet: „u2(t) = x + y sin (omega t)” Olvasva: x feszültséggel eltolt y sin (omega t) szinuszfeszültség. Nem az y az AC! Ha már így nevezed.
A bemenet egy ugrás függvény volt, a rendszer pedig csak egy energiatárolót tartalmaz(nem tud ide oda áramlani az energia--> nem alakulhat ki lengés), így lehetetlen hogy a kimeneten szinuszos jel jelenjen meg.
Idézet: „Olvasva: x feszültséggel eltolt y sin (omega t) szinuszfeszültség. Nem az y az AC! Ha már így nevezed.” Nem én nevezem így, hanem a tanár. Itt van leírva feketén-fehéren egy példa: u(t) = 10 + 10 sin (2omega t + pi/6), ahol az első (10) szám a DC, a második az AC tag.
Az változtat valamit, ha találtam egy hasonló példát, de ott meg van adva, hogy t=0, t=1us, és t=végtelen időpillanatokban kell nézni az eredményt?
Miért változtatna? Meg van az időfüggvény, a kérdéses időpillanatokat beleírod, aztán kijön az eredmény. Ha végtelen az idő, akkor a kondenzátor olyan mintha ott sem lenne(feltöltődött teljesen), így ugyanakkora feszültség fog kijönni, mintha a feszültségosztó képletét használnád.
Azért ott van, hogy: a második tag. Ahol a y nem csak a 10, hanem az egész kifejezés.
Egy 12 us -os periódus idejű szinuszhullámot nemigen szoktunk AC -nek nevezni. Ezt többnyire a hálózati frekvenciára értjük.
Miért ne neveznénk?
AC ->alternating current. Frekvencia lényegtelen kivéve ha 0, mert akkor DC  . Igaz, hogy a gyakorlatban leginkább az 50Hz van jelen, de elméletben bármilyen frekvenciájú szinuszt nevezhetünk így. Ha még lazábban értelmezzük még szinusznak sem kell, hogy legyen, egy háromszög, négyszög jel is lehet AC ha nem nullára ültetett, hanem negatív és pozitív periódusa is van. . Igaz, hogy a gyakorlatban leginkább az 50Hz van jelen, de elméletben bármilyen frekvenciájú szinuszt nevezhetünk így. Ha még lazábban értelmezzük még szinusznak sem kell, hogy legyen, egy háromszög, négyszög jel is lehet AC ha nem nullára ültetett, hanem negatív és pozitív periódusa is van.
Egy adatlapon vannak egyenáramú adatok: "DC Characteristics" Tápfeszültség, felvett áram, stb. Vannak más adatok (direkt nem írom a magyar kifejezést): AC Characteristics. Ez utóbbiban szerepel pl. a maximális kapcsolási frekvencia néha többszáz MHz...
Mindenesetre fura ízlésed van. Az AC az erősáramú technikában használt kifejezés, rövidítés, az áramrendszereket nevezik így. A gyengeáramú hálózatoknál nem használatos. (legalábbis eddig nem)
A 12 us periódus idejű szinusz feszültség egyrészt nem áram, másrészt a 83 kHz -et nem nevezném hálózati frekvenciának. Léteznek 16 2/3, 25, 50, 60, 400 Hz -es hálózati frekvenciák, amiket általánosan, viszonylag gyakran használnak.
Az Angol nyelvú szakirodalom így ismeri: AC analysis. Többen vannak...
Nem beszéltem hálózati frekvenciáról, csak frekvenciáról, de mindegy.
Mint Hp41C is megerősítette és mint a belinkelt találatok mutatják, nem csak a hálózati 50Hz az AC, de mivel ezzel nem sokat segítünk a kérdezőnek nem is offolok tovább. 
Egyértelmű, hogy az AC-hoz a szám és az az utáni dolgok tartoznak (amik leírják a fázist). De a DC rész az tényleg csak a szám.
Ismét kérnék egy kis segítséget.
Az alábbi feladattal az a fő problémám, hogy az egyes értékek nem egy, hanem két tagból állnak, és az ω érték sem a megszokott egyszeres, ráadásul nincs fázistolás, amiből számolni lehetne a komplex értékeket. A feladat: u(t) = 2 + 3 sin(ωt) + 4 cos(3ωt) [V] i(t) = 2 sin(ωt) + 3 sin(3ωt) [A] A kérdés a komplex teljesítmény a fenti két érték alapján. Mi lenne a számolás menete?
A fő gondom az, hogy a komplex teljesítményhez a feszültséget és az áramot is komplex alakra kéne hozni. Ehhez a képlet:
U*sin(ωt+φ) -> U*(sinφ + j cosφ) Mivel a fenti esetben nincs φ, ha nullával számolok (cos 0 és sin 0), akkor a valós részre mindig nulla fog kijönni, ami hibás. Ráadásul u(t)-ben a második érték cos-os, nem sin-os (4 cos(3ωt)). Ezzel (és a háromszoros ω-val) mit kéne kezdeni?
Szerintem külön külön kell meghatározni mindegyik tagra és a végén összeadni(szuperpozíció). A koszinusz meg ugyanaz mint a szinusz csak 90°-kal el van tolva.
Erre gondoltam én is, de ha egyszer a φ nem szerepel a tagokban (vagyis nem tudjuk az értékét), akkor nem tudom komplex alakra hozni őket. :S
Mondjuk az első példánál az u(t) így nézne ki, ha a fíket is beleírod:
u(t) = 2 + 3 sin(ωt) + 4 cos(3ωt) [V] = 2sin(0t+90°)+3sin(ωt+0°)+4sin(3ωt+90°) [V] Remélem jól csináltam, kicsit most fáradt vagyok. Ha kíváncsi vagy ennek a jelnek a jelalakjára akkor pl excellel ki tudod rajzoltatni, ugyanezt látnád egy oszcilloszkóp képernyőjén ha ezt a jelet előállítanánk(ez nem teljesen szinuszos alakú lesz). Például egy négyszögjelet(vagy bármilyen periodikus jelet) is fel lehet bontani ilyen szinuszos tagok összegére(Fourier-sor). A hozzászólás módosítva: Máj 27, 2014
Nekem már rég volt, de valami olyasmi rémlik, hogy csak az azonos frekvenciájú komponensek hoznak létre teljesítményt.
Itt tehát DC teljesítmény nincs, mert a DC áram 0. Ezen kívül lesz egy ω és egy 3ω frekvenciájú teljesítmény összetevő. A φ pedig 0, így lehet vele számolni: sin0=0, cos0=1. Sajnos csak ennyire emlékszem, erre sem üzembiztosan, úgyhogy tévedhetek is...
Szerintem bambán össze kell szorozni.
p(t)=u(t)*i(t)=[2+3sin(ωt) + 4cos(3ωt)] * [2sin(ωt) + 3sin(ωt)] A feszültség egy 2 egységgel eltolt (egyenszint) 3 egység amplitúdójú szinuszhullám, és egy négy egység amplitúdójú háromszoros frekvenciájú 90 fokban eltolt (cos) feszültségek összege. (ez olyan sarkos, négyszögjelhez hasonló jelalak) Az áram egy 2 egység amplitúdójú, szinuszos áram, és egy a vele azonos fázisban levő 3 egység amplitúdójú 3 szoros frekvenciájú áramok összege. Ha a két - két tagot összeszorzod, kapsz egy elég hosszú polinomot, amit aztán egyszerűsíthetsz, vagy nem, mindenesetre épkézláb formára hozhatod. Nem biztos, hogy bele kell keverni a komplex számokat, de nincs kizárva, mert biztos lesznek benne négyzetes tagok. Sok sikert a számolgatáshoz.
Az iskolában kaptam egy feladatott ami számomra fontos mivel ettől függ elektorenergetikai jegyem és az értesítő könyvem jegye is ettől függ. Kaptam áramköröket és elkel magyaráznom működésüket,?
A rajzokat mellékletben csatolom. Birtok segíteni elmagyarázni működésüket? Keddre kellene. A képek alatt szerb szöveg van, de az lényegtelen,emígy a fordításban benne van a fordítás . előre is köszönöm. A hozzászólás módosítva: Máj 28, 2014
|
Bejelentkezés
Hirdetés |
A használat feltételei
• Adatvédelem
• GY.I.K., Használati útmutató és szabályok
• Impresszum
• Elosztó
• Hiba jelentése
K�rlek v�rj...